ganzrationale Funktionen
Wendepunkte und Krümmung
Einleitung
Wendepunkte berechnen
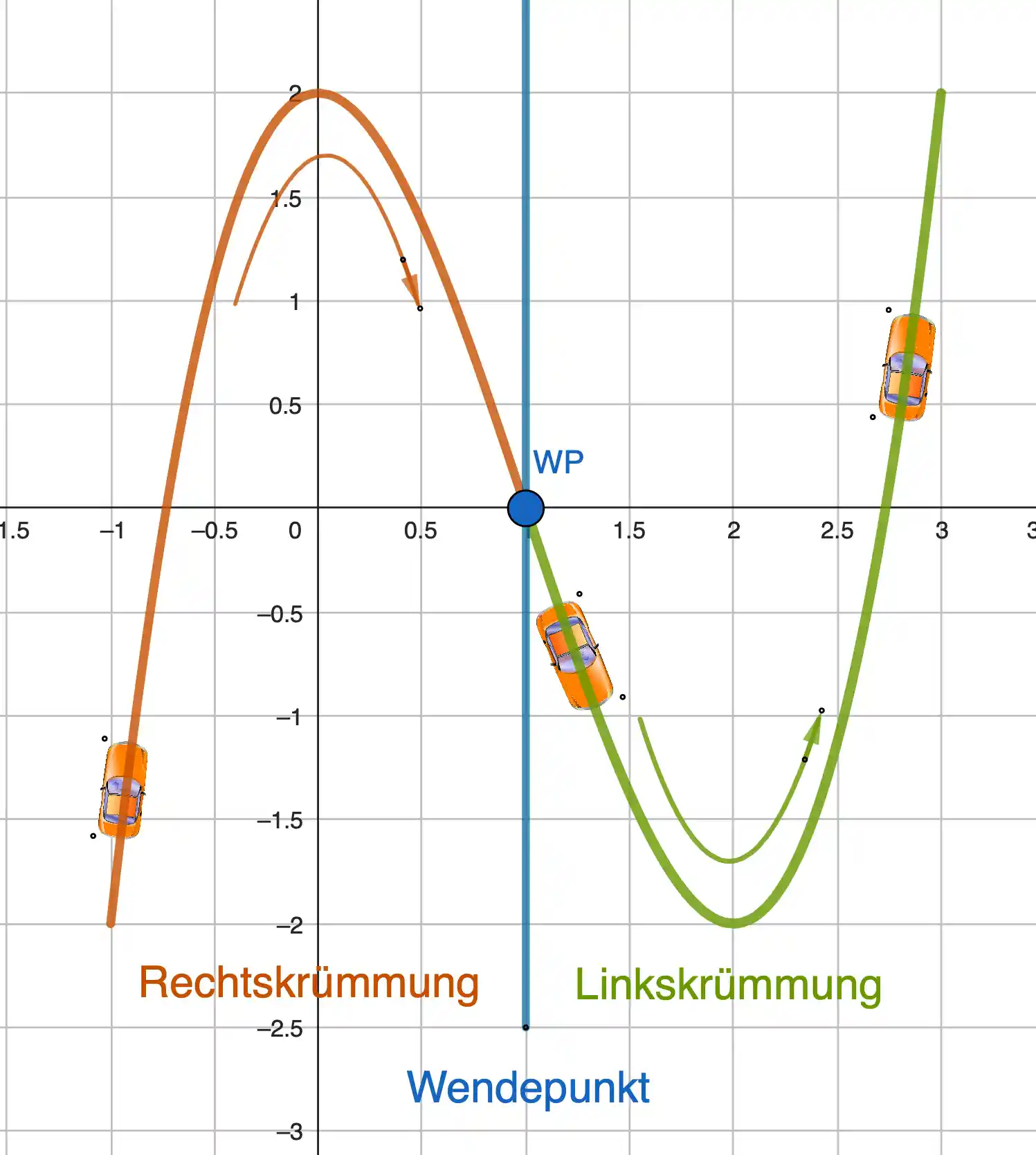
Krümmung am Graphen erkennen
Stell dir einmal vor, du hättest keine Funktion vor dir, sondern würdest von oben auf eine Straße schauen. Wenn du diese Straße entlangfährst, hat sie Rechtskurven und Linkskurven. Das sind die Krümmungsbereiche.
Die Bereiche, in denen du eine Rechtskurve fährst, nennt man rechtsgekrümmt.
Die Bereiche, in denen du eine Linkskurve fährst, nennt man linksgekrümmt.
Die roten Bereiche sind die, in denen du eine Rechtskurve fährst. Man nennt sie rechtsgekrümmt.
Die grünen Bereiche sind die, in denen du eine Linkskurve fährst. Man nennt sie linksgekrümmt.
Betrachten wir nun die Bereiche etwas genauer und lesen die Stellen ab, an denen sie beginnen und enden. So bestimmen wir die Krümmungsintervalle.
Dort, wo ein Wechsel der Krümmung stattfindet, liegen die Wendepunkte der Funktion. Rechtsgekrümmt und danach linksgekrümmt ⇒ dazwischen liegt ein Wendepunkt.
Übertragen wir dieses Wissen auf unseren Beispielgraphen:
Möchtest du die Krümmungsintervalle bestimmen, ohne den Graphen der Funktion gegeben zu haben, musst du die 2.Ableitung betrachten. Sie erzählt dir alles über Krümmung und Wendepunkte einer Funktion.
Krümmungsverhalten → beschreibt, ob eine Funktion linksgekrümmt oder rechtsgekrümmt ist.
Die 2.Ableitung erzählt dir alles über Krümmung und Wendepunkte einer Funktion.
Krümmung und Wendepunkte mit der Vorzeichentabelle bestimmen
Du hast gelernt, die Wendepunkte mithilfe der 2.Ableitung und 3.Ableitung zu bestimmen.
Es gibt aber noch eine andere Möglichkeit, die dir gleichzeitig einen Überblick über das Krümmungsverhalten gibt:
die Vorzeichentabelle. Diese Methode erspart dir außerdem die 3.Ableitung.
Wir gehen das Ganze Schritt für Schritt an unserem Beispiel durch.
Leite die Funktion zweimal ab und berechne die Nullstellen von \( f''(x) \):
Jetzt nutzen wir nicht die 3.Ableitung, sondern legen eine Vorzeichentabelle für \( f''(x) \) an. Das bedeutet, wir betrachten die Bereiche links und rechts der berechneten Nullstelle \( {\textcolor{orange}{x_0 = 1}} \):
- links von \( {\textcolor{orange}{1}} \) → wir setzen \( 0 \) ein
- rechts von \( {\textcolor{orange}{1}} \) → wir setzen \( 2 \) ein
\( \begin{array}{c|c|c|c} x & x < {\textcolor{orange}{x_0}} & {\textcolor{orange}{x_0}} & x > {\textcolor{orange}{x_0}} \\ \hline f''(x) & & 0 & \end{array} \)
An der Stelle \( {\textcolor{orange}{x_0}} \) setzen wir das Ergebnis unserer Nullstellenberechnung ein, also \( {\textcolor{orange}{1}} \).
Dann ergänzen wir einen kleineren x-Wert und einen größeren x-Wert...
\( \begin{array}{c|c|c|c} x & 0 & {\textcolor{orange}{1}} & 2 \\ \hline f''(x) & & 0 & \\ \end{array} \)
... und setzen diese Werte in die 2.Ableitung ein, um die Tabelle zu füllen:
\( \begin{array}{c|c|c|c} x & 0 & {\textcolor{orange}{1}} & 2 \\ \hline f''(x) & -6 & 0 & 6 \\ \end{array} \)
In einer zusätzlichen Zeile ergänzen wir das Vorzeichen der 2.Ableitung in den einzelnen Bereichen. Diese Zeile zeigt dir, ob die 2.Ableitung dort positiv oder negativ ist.
Das Vorzeichen der 2.Ableitung sagt dir, ob die Funktion linksgekrümmt oder rechtsgekrümmt ist. Sie erklärt uns das Krümmungsverhalten.
- \( f''(x) \gt 0 \) → LK: linksgekrümmt
- \( f''(x) \lt 0 \) → RK: rechtsgekrümmt
- \( f''(x) = 0 \) → mögliche Wendestelle (WP)
Dieses Wissen wenden wir jetzt auf unsere Funktion an:
\( \begin{array}{c|c|c|c} x & 0 & {\textcolor{orange}{1}} & 2 \\ \hline f''(x) & -6 & 0 & 6 \\ \hline & {\textcolor{orangered}{-}} & 0 & {\textcolor{green}{+}} \\ \hline & {\textcolor{orangered}{\text{RK}}} & \textsf{WP} & {\textcolor{green}{\text{LK}}} \end{array} \)
Damit ist klar, dass \( {\textcolor{orange}{x_0 = 1}} \) eine Wendestelle ist. Nun bleibt noch die y-Koordinate zu berechnen:
Dank der Tabelle können wir:
- sicher sagen, dass bei \( {\textcolor{orange}{x_0 = 1}} \) eine Wendestelle ist
- die Krümmungsintervalle ablesen
- \( f''(x) \gt 0 \) → Die Funktion ist linksgekrümmt
- \( f''(x) \lt 0 \) → Die Funktion ist rechtsgekrümmt
- \( f''(x) = 0 \) → Möglicher Wendepunkt
Findest du es auch schwierig, dir zu merken, wann der Graph linksgekrümmt und wann er rechtsgekrümmt ist?
Schau mal, wir haben da vielleicht etwas, das dir dabei hilft.
- \( f''(x) \lt 0 \) → Rechtskrümmung (trauriger Mund ↓)
- \( f''(x) \gt 0 \) → Linkskrümmung (fröhlicher Mund ↑)
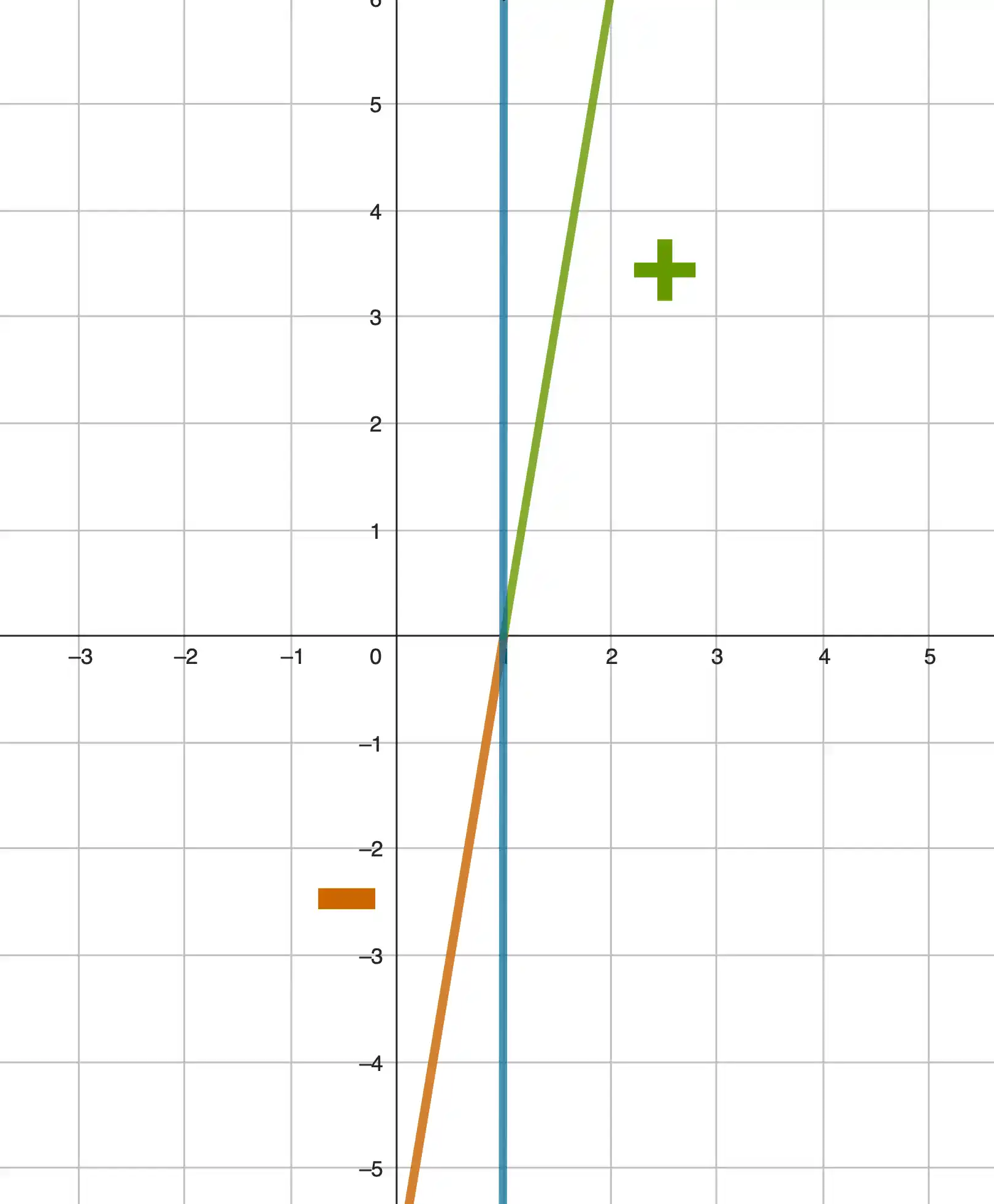
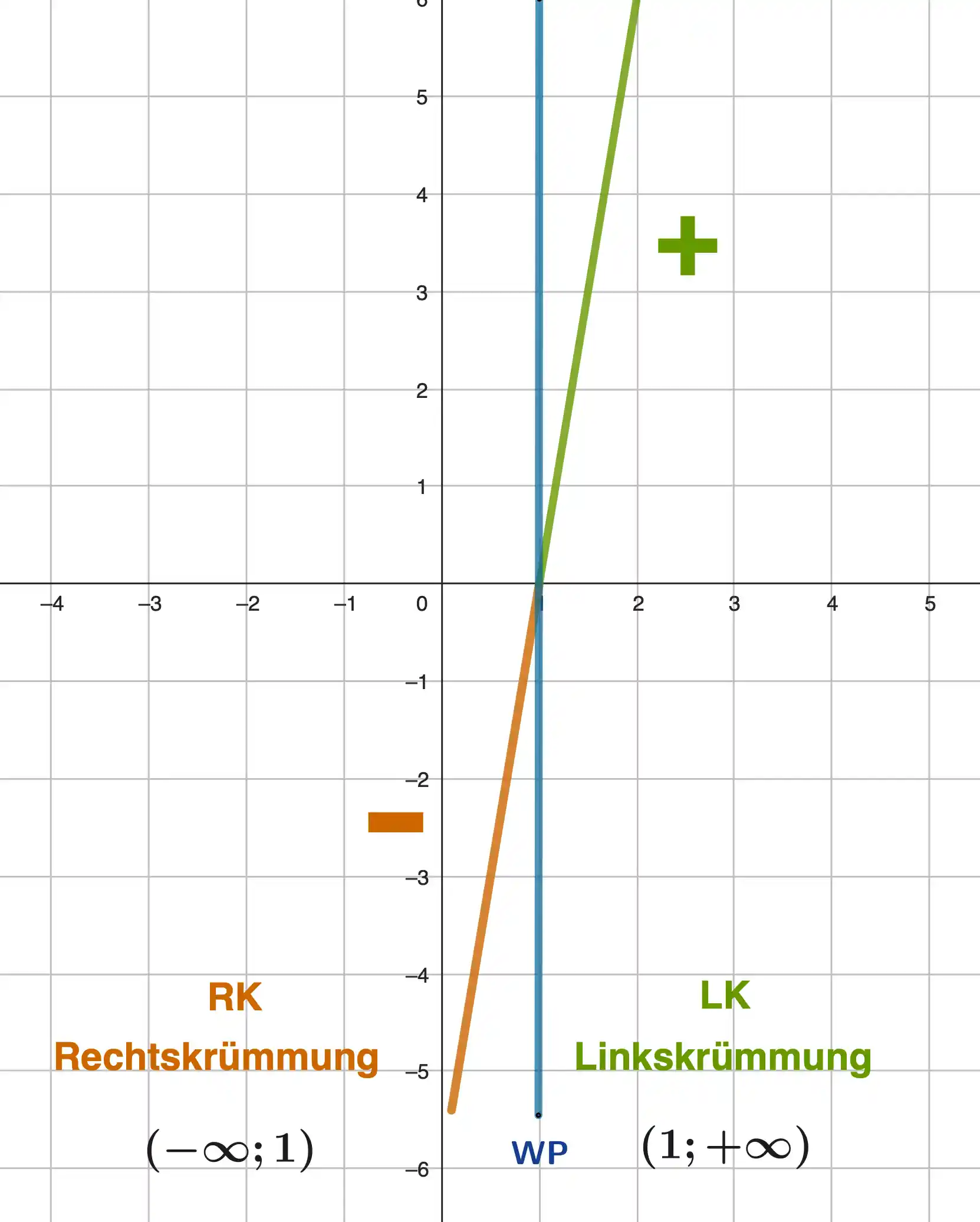
Krümmung am Graphen der 2.Ableitung ablesen
Es gibt noch eine weitere Variante, das Krümmungsverhalten und die Wendestellen zu bestimmen: Dazu schauen wir uns den Graphen der 2.Ableitung an.
Die ersten Schritte bleiben gleich – Funktion zweimal ableiten und die Nullstellen der 2.Ableitung bestimmen.
Jetzt notieren wir uns die Nullstelle von \( f''(x) \) und schauen uns den groben Verlauf dieser 2.Ableitung an. Um den groben Verlauf zu bestimmen, interessiert uns nur der höchste Exponent und das Vorzeichen seines Summanden. Hier ist \( f''(x)=6x-6 \) eine steigende Gerade (höchster Exponent \( 1 \), positives Vorzeichen).
Mit diesen Informationen können wir eine Skizze der 2.Ableitung anfertigen.
Wie du siehst, hat die 2.Ableitung Bereiche, in denen sie positiv (oberhalb der x-Achse) ist, und Bereiche, in denen sie negativ (unterhalb der x-Achse) ist.
Das sind die Informationen, die wir brauchen, um die Krümmungsintervalle zu bestimmen.
- \( f''(x) \gt 0 \) → linksgekrümmt
- \( f''(x) \lt 0 \) → rechtsgekrümmt
- \( f''(x) = 0 \) → mögliche Wendestelle (Vorzeichenwechsel prüfen)
In unserem Bild stehen nun alle Informationen, die wir brauchen:
Links von \( {\textcolor{orange}{1}} \) ist die 2.Ableitung negativ, also rechtsgekrümmt,
rechts davon ist sie positiv, also linksgekrümmt.
Dazwischen, bei \( {\textcolor{orange}{1}} \), liegt der Wendepunkt.
Ergebnis:
→ Der Verlauf der 2.Ableitung zeigt dir Krümmung und Wendestellen:
- \( f''(x) \) über der x-Achse → positiv → linksgekrümmt
- \( f''(x) \) unter der x-Achse → negativ → rechtsgekrümmt
- \( f''(x) \) hat eine Nullstelle und wechselt das Vorzeichen → Wendepunkt
Zusammenfassung
Du suchst Profi-Nachhilfe mit echtem Impact? Dann bist du bei OnMathe genau richtig!
Ausgewählt für Dich
Empfohlene Beiträge
Mehr dazu
in unseren FAQs
Was ist ein Wendepunkt?
Ein Wendepunkt ist der Punkt, an dem der Graph einer Funktion seine Krümmung ändert – also von rechtsgekrümmt zu linksgekrümmt oder umgekehrt.
Wie erkenne ich Wendepunkte rechnerisch?
Du berechnest die 2.Ableitung und findest ihre Nullstellen. Liegt dort ein Vorzeichenwechsel vor (oder die 3.Ableitung ist ungleich null), handelt es sich um eine Wendestelle.
Worin liegt der Unterschied zwischen rechts- und linksgekrümmt?
Rechtsgekrümmt bedeutet, der Graph biegt sich wie eine Rechtskurve, linksgekrümmt wie eine Linkskurve. In den Bereichen dazwischen kann ein Wendepunkt liegen.
Brauche ich immer die 3.Ableitung, um Wendepunkte zu bestimmen?
Nein, du kannst auch mit einer Vorzeichentabelle der 2.Ableitung arbeiten oder den Graphen der 2.Ableitung betrachten. Die 3.Ableitung ist nur eine von mehreren Methoden.
Was bedeuten Krümmungsintervalle?
Krümmungsintervalle sind die Bereiche, in denen der Graph durchgehend rechtsgekrümmt oder linksgekrümmt ist. An den Grenzen dieser Intervalle liegen die Wendepunkte.
Vertiefung
Weiterführende Informationen
Wendepunkte und Krümmung als Werkzeug
Wendepunkte und Krümmung sind zentrale Werkzeuge in der Analysis. Sie helfen dir, das Verhalten von Funktionen genau zu beschreiben und zu verstehen, wie sich ein Graph im Verlauf verändert.
Was sind Wendepunkte und Krümmung?
Ein Wendepunkt ist die Stelle, an der eine Funktion ihr Krümmungsverhalten ändert. Die Krümmung gibt an, ob der Graph linksgekrümmt oder rechtsgekrümmt verläuft. Mit Wendepunkten und Krümmung kannst du also erkennen, ob eine Funktion nach links oder nach rechts gebogen ist.
Mathematische Bedeutung
Wendepunkte und Krümmung sind wichtig, um das exakte Aussehen eines Funktionsgraphen zu beschreiben. Sie ergänzen Hochpunkte, Tiefpunkte und Symmetrien und sind unverzichtbar für eine vollständige Kurvendiskussion. Besonders in Physik, Technik oder Wirtschaft spielen Wendepunkte eine Rolle, wenn es darum geht, Veränderungen im Verlauf von Prozessen zu verstehen.
Typische Fehler und Lerntipps
Ein häufiger Fehler ist es, nur die Nullstellen der 2.Ableitung zu berechnen, ohne das Vorzeichen zu prüfen. So entstehen falsche Wendepunkte. Denke daran: Nur wenn die 2.Ableitung an der Stelle das Vorzeichen wechselt oder die 3.Ableitung ungleich null ist, liegt wirklich ein Wendepunkt vor. Als Lerntipp: Erstelle dir kleine Vorzeichentabellen oder Skizzen, um Krümmung und Wendepunkte sicher zu erkennen.
Ursprung und Entwicklung
Die Untersuchung von Wendepunkten und Krümmung entstand zusammen mit der Entwicklung der Differentialrechnung im 17. Jahrhundert. Mathematiker wie Isaac Newton und Gottfried Wilhelm Leibniz haben Methoden entwickelt, mit denen man Krümmungen systematisch bestimmen kann.
Moderne Anwendung
Heute nutzt man Wendepunkte und Krümmung in vielen Bereichen: in der Technik, um Materialbelastungen vorherzusagen, in der Wirtschaft, um Wachstumsprozesse zu analysieren, oder in der Informatik bei der Modellierung von Funktionen. Auch in der Schule bleibt das Verständnis von Wendepunkten und Krümmung ein Schlüsselthema, weil es dir hilft, Graphen vollständig zu beschreiben.
