ganzrationale Funktionen
Extrempunkte und Monotonie
Einleitung
Extrempunkte bestimmen mit der 2. Ableitung
Monotonieverhalten erkennen
Ist der Graph der Funktion gegeben, kannst du diese Bereiche ablesen.
Die roten Bereiche sind die Bereiche, in denen die Funktion fällt - sie ist streng monoton fallend.
Betrachten wir nun die Bereiche etwas genauer, und lesen die Stellen ab, an denen sie beginnen und enden. So bestimmen wir die Monotonieintervalle. Ergebnis:
Wie genau das geht, lernen wir in den nächsten Abschnitten.
Die 1. Ableitung erzählt dir alles über Monotonie und Extrempunkte einer Funktion.
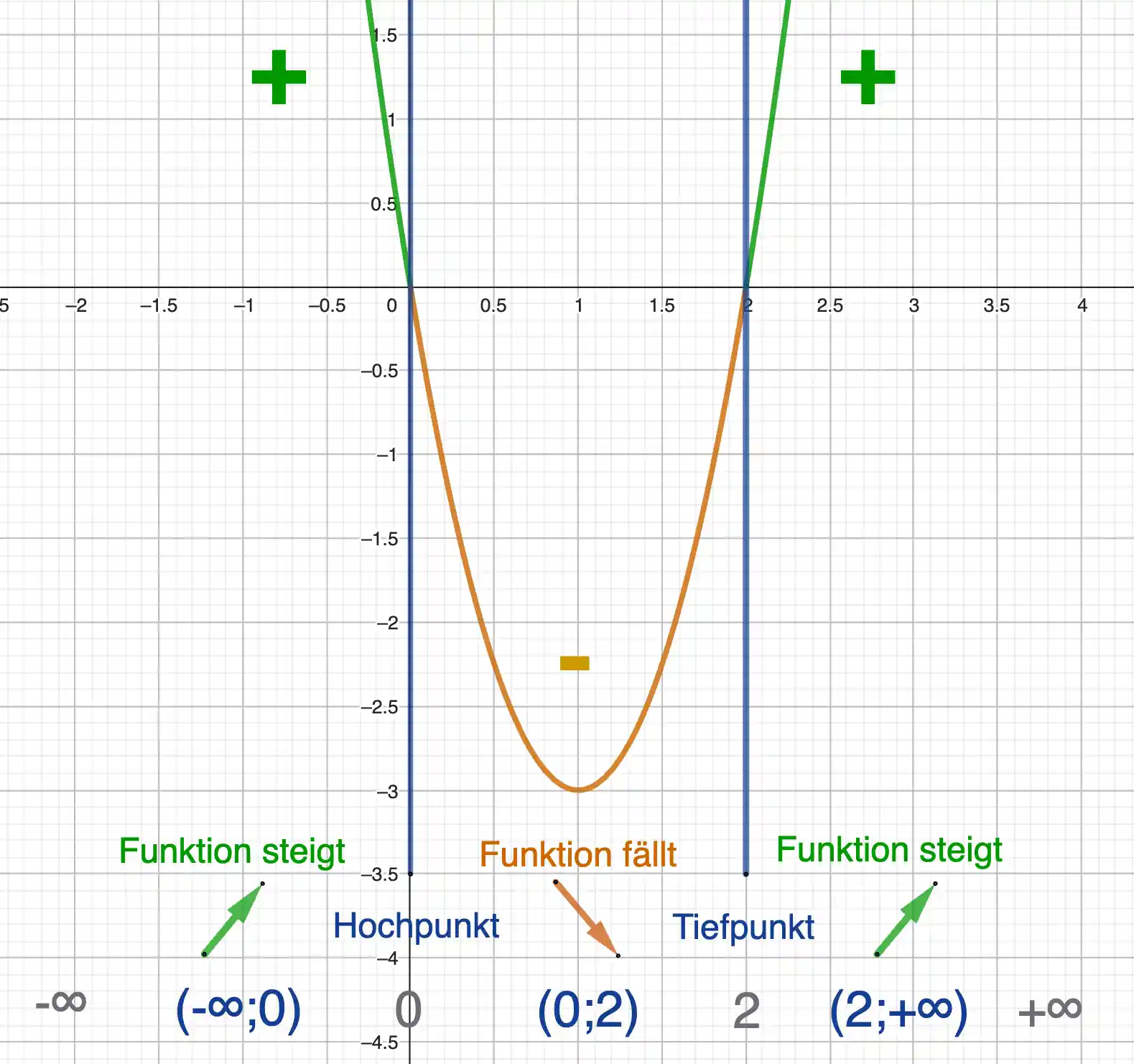
Die Vorzeichentabelle nutzen
Eine Variante ist die Vorzeichentabelle. Sie ist vor allem dann interessant, wenn du auch einen Überblick über das Monotonieverhalten bekommen möchtest. Diese Methode erspart dir außerdem die 2. Ableitung.
Wir gehen das ganze Schritt für Schritt an unserem Beispiel durch.
- links von \( {\textcolor{orange}{0}} \)
- zwischen \( {\textcolor{orange}{0}} \) und \( {\textcolor{green}{2}} \)
- rechts von \( {\textcolor{green}{2}} \)
\( \begin{array}{c|c|c|c|c|c} x & x < {\textcolor{orange}{x_1}} & {\textcolor{orange}{x_1}} & {\textcolor{orange}{x_1}} < x > {\textcolor{green}{x_2}} & {\textcolor{green}{x_2}} & x > {\textcolor{green}{x_2}} \\ \hline f'(x) & & 0 & & 0 \end{array} \)
Jetzt ergänzen wir die fehlenden x-Werte...
\( \begin{array}{c|c|c|c|c|c} x & -1 & {\textcolor{orange}{0}} & 1& {\textcolor{green}{2}} & 3\\ \hline f'(x) & & 0 & & 0 & \end{array} \)
\( \begin{array}{c|c|c|c|c|c} x & -1 & {\textcolor{orange}{0}} & 1& {\textcolor{green}{2}} & 3\\ \hline f'(x) & 9 & 0 & -3 & 0 & 9 \end{array} \)
- \( f'(x) > 0 \) → \( f(x) \) ist steigend \(\quad \nearrow\)
- \( f'(x) < 0 \) → \( f(x) \) ist fallend \(\quad \searrow\)
- \( f'(x) = 0 \) → möglicher Extrempunkt
Ergebnis:
- \( f'(x) > 0 \) → Funktion ist streng monoton steigend
- \( f'(x) < 0 \) → Funktion ist streng monoton fallend
- \( f'(x) = 0 \) → Möglicher Extrempunkt (weiter prüfen!)
Monotonie am Graphen der Ableitung erkennen
Das ist die Information, die wir brauchen, um das Monotonieverhalten der Funktion abzulesen.
- \( f'(x) > 0 \) → \( f(x) \) ist steigend \(\quad \nearrow\)
- \( f'(x) < 0 \) → \( f(x) \) ist fallend \(\quad \searrow\)
- \( f'(x) = 0 \) → möglicher Extrempunkt
- Die Ableitung ist positiv (oberhalb der x-Achse) - die Funktion ist streng monoton steigend
- Die Ableitung ist negativ (unterhalb der x-Achse) - die Funktion ist streng monoton fallend
- Die Ableitung hat eine Nullstelle - die Funktion hat einen Extrempunkt
Zusammenfassung
- Extrempunkte sind Hoch- oder Tiefpunkte einer Funktion.
- Sie liegen an den Nullstellen der ersten Ableitung.
- Ob Hoch- oder Tiefpunkt? → Schau auf das Vorzeichen von \(f''(x)\) oder nutze eine Vorzeichentabelle.
- Monotonie gibt an, ob die Funktion steigt oder fällt.
- Sie hängt vom Vorzeichen der Ableitung \(f'(x)\) ab:
- \(f'(x) > 0\) → Funktion steigt
- \(f'(x) < 0\) → Funktion fällt
- Mit einer Vorzeichentabelle kannst du alle Monotonieintervalle einfach erkennen.
Gegeben ist die Funktion:
1. Ableitung:
Nullstellen der Ableitung berechnen → mögliche Extrempunkte:
2. Ableitung aufstellen und prüfen:
Monotonie:
- fallend für \( x \lt -\sqrt{2} \)
- steigend für \( x \gt -\sqrt{2} \) bis \( x \lt \sqrt{2} \)
- steigend für \( x \gt \sqrt{2} \)
Die Ableitung zeigt dir, wie sich die Funktion verhält:
- \( f'(x) = 0 \) → mögliche Extremstelle
- \( f''(x) > 0 \) → Tiefpunkt
- \( f''(x) < 0 \) → Hochpunkt
- \( f'(x) > 0 \) → Funktion steigt
- \( f'(x) < 0 \) → Funktion fällt
Du suchst Profi-Nachhilfe mit echtem Impact? Dann bist du bei OnMathe genau richtig!
Ausgewählt für Dich
Empfohlene Beiträge
Mehr dazu
in unseren FAQs
1. Was sind Extrempunkte überhaupt?
Extrempunkte sind Stellen, an denen ein Graph seinen höchsten oder tiefsten Punkt in einem bestimmten Bereich hat. Man unterscheidet zwischen Hochpunkten und Tiefpunkten.
2. Woran erkennt man, ob ein Punkt ein Hoch- oder Tiefpunkt ist?
Das erkennt man am Verhalten des Graphen davor und danach: Steigt er vor dem Punkt und fällt danach, ist es ein Hochpunkt – umgekehrt ein Tiefpunkt.
3. Was bedeutet Monotonie bei Funktionen?
Monotonie beschreibt, ob ein Graph steigt oder fällt. Eine Funktion ist monoton steigend, wenn sie immer weiter nach oben geht, und monoton fallend, wenn sie nach unten geht.
4. Welche Rolle spielt die Ableitung bei Extrempunkten und Monotonie?
Die Ableitung zeigt an, ob eine Funktion gerade steigt, fällt oder einen Extrempunkt hat. Ist die Ableitung null, liegt ein möglicher Extrempunkt vor.
5. Was ist der Unterschied zwischen lokalem und globalem Extrempunkt?
Ein lokaler Extrempunkt ist nur in einem kleinen Bereich der höchste oder tiefste Punkt. Ein globaler Extrempunkt ist der höchste oder tiefste Punkt der ganzen Funktion.
Vertiefung
Weiterführende Informationen
Extrempunkte und Monotonie als Werkzeug der Mathematik
Extrempunkte und Monotonie sind zentrale Werkzeuge der Analysis, mit denen du das Verhalten von Funktionen gezielt untersuchen kannst. Sie helfen dir zu erkennen, wann eine Funktion wächst, wann sie fällt und wo sie ihr Maximum oder Minimum erreicht. Stell dir vor, du beobachtest einen Wanderweg in den Bergen: Die Gipfel und Täler auf der Route entsprechen den Hoch- und Tiefpunkten, die Steigung oder das Gefälle zeigen dir die Monotonie. Genau wie in der Natur ist es auch in der Mathematik wichtig zu wissen, wie sich etwas entwickelt. In diesem Beitrag lernst du, wie du Extrempunkte und Monotonie bestimmst, was sie dir über Funktionen verraten und wie du sie sinnvoll einsetzt, um auch komplexe Zusammenhänge zu verstehen.
Was sind Extrempunkte und Monotonie?
Extrempunkte sind Stellen auf dem Graphen einer Funktion, an denen ein lokales oder globales Maximum oder Minimum erreicht wird. Das bedeutet: Hier ändert sich das Verhalten der Funktion – sie wechselt von steigend zu fallend oder umgekehrt. Die Monotonie beschreibt dagegen, ob eine Funktion in einem bestimmten Bereich nur steigt oder nur fällt. Gemeinsam liefern Extrempunkte und Monotonie eine Art Fahrplan für den Verlauf einer Funktion und sind damit ein unverzichtbarer Teil jeder Kurvendiskussion. Indem du das Verhalten der Funktion in bestimmten Intervallen untersuchst, gewinnst du ein genaues Bild ihrer Struktur.
Die mathematische Bedeutung
In der Mathematik spielen Extrempunkte und Monotonie eine bedeutende Rolle, besonders im Zusammenhang mit Ableitungen und der Analyse von Funktionen. Sie helfen nicht nur dabei, einen Graphen korrekt zu skizzieren, sondern sind auch der Schlüssel zu vielen Anwendungsaufgaben. Ob in der Wirtschaft zur Gewinnmaximierung, in der Biologie zur Beschreibung von Wachstumsprozessen oder in der Technik zur Optimierung von Abläufen – überall, wo etwas maximiert oder minimiert werden soll, kommen Extrempunkte ins Spiel. Die Monotonie liefert zusätzlich Informationen darüber, in welchen Bereichen eine Funktion durchgängig wächst oder sinkt, was bei der Interpretation von Funktionen entscheidend ist.
Häufige Fehler vermeiden
Ein häufiger Fehler beim Umgang mit Extrempunkten und Monotonie ist die Annahme, dass jede Stelle mit waagerechter Tangente automatisch ein Hoch- oder Tiefpunkt ist. In Wahrheit kann es sich auch um einen sogenannten Sattelpunkt handeln, bei dem die Funktion ihr Verhalten nicht ändert. Ebenso werden Monotonieintervalle oft nicht korrekt angegeben, wenn die Ableitung zwar null ist, aber keine wirkliche Verhaltensänderung erfolgt. Um solche Fehler zu vermeiden, solltest du immer das Vorzeichen der Ableitung in den benachbarten Werten der Nullstellen der ersten Ableitung überprüfen. Auch das falsche Eintragen in Steigungstabellen oder ungenaue Skizzen führen schnell zu Missverständnissen. Übung und ein klares System helfen, solche Stolpersteine aus dem Weg zu räumen.
Wenn du hierfür Unterstützung suchst, hilft dir gerne einer der Profi-Tutoren mit effektiver Mathe Nachhilfe online.
Tipps für effektives Lernen
Um Extrempunkte und Monotonie sicher zu beherrschen, solltest du regelmäßig mit echten Funktionsbeispielen arbeiten. Zeichne dir Steigungstabellen, um das Verhalten übersichtlich darzustellen, und übe das Einordnen von Hoch- und Tiefpunkten in verschiedenen Kontexten. Es hilft auch, dir den Verlauf bildlich vorzustellen – wie bei einer Bergwanderung, bei der du erkennst, wann du bergauf oder bergab gehst. Achte besonders darauf, wie sich die Ableitung in bestimmten Bereichen verhält, und lerne typische Funktionsverläufe kennen. Gruppenarbeit, digitale Tools oder Nachhilfevideos können dich zusätzlich dabei unterstützen, das Thema aus verschiedenen Blickwinkeln zu verstehen.
Ursprünge von Extrempunkten und Monotonie
Die Analyse von Extrempunkten und Monotonie geht zurück auf die Anfänge der Differentialrechnung im 17. Jahrhundert. Mathematiker wie Isaac Newton und Gottfried Wilhelm Leibniz entwickelten die ersten Methoden, um mit Hilfe von Ableitungen das Verhalten von Funktionen zu untersuchen. Ihre Ideen legten den Grundstein für viele moderne Analysetechniken. Während die Konzepte damals noch mit geometrischen Überlegungen verbunden waren, entwickelte sich daraus bald ein klarer systematischer Zugang, der bis heute in der Schule gelehrt wird. Die Untersuchung von Hoch- und Tiefpunkten war eines der ersten großen Anwendungsfelder der neu entstandenen Infinitesimalrechnung.
Extrempunkte und Monotonie in der modernen Mathematik
Heute sind Extrempunkte und Monotonie fester Bestandteil der Mathematik und finden in vielen Bereichen Anwendung. In der Wirtschaft helfen sie, Kosten zu minimieren oder Gewinne zu maximieren. In der Technik werden Maschinenprozesse damit optimiert, und in den Naturwissenschaften lassen sich natürliche Prozesse besser beschreiben. Auch in der Informatik und der künstlichen Intelligenz spielen sie eine Rolle, zum Beispiel bei der Optimierung von Algorithmen. Ihre Bedeutung liegt vor allem darin, dass sie grundlegende Einsichten liefern – über das Verhalten, die Struktur und die Entwicklung mathematischer Zusammenhänge. Wer dieses Werkzeug beherrscht, ist in der Lage, weit über das Schulwissen hinaus mathematisch zu denken und zu handeln.
