Alles über Nullstellen
Nullstellen - Arten & Vielfachheit
Einleitung
- einfache Nullstelle, Schnittpunkt: \(x \ \textsf{oder} \ (x-x_0)\)
- doppelte Nullstelle, Berührpunkt: \(x^2 \ \textsf{oder} \ (x-x_0)^2\)
- dreifache Nullstelle, Sattelpunkt: \(x^3 \ \textsf{oder} \ (x-x_0)^3\)
Arten von Nullstellen
Es gibt 3 Arten von Nullstellen. Sie unterscheiden sich in ihrer Vielfachheit. Wir gehen sie schrittweise durch.
Einfache Nullstellen
Eine einfache Nullstelle ist eine Nullstelle, bei der die Funktion die x-Achse schneidet. Das bedeutet auch, dass das Vorzeichen der Funktion um die Nullstelle herum wechselt.
In einer Funktionsgleichung könnte das so aussehen:- \(f(x)=x\)
- \(f(x)=x-2\)
Doppelte Nullstellen
Eine doppelte Nullstelle ist eine Nullstelle, bei der die Funktion die x-Achse berührt. Das bedeutet auch, dass das Vorzeichen der Funktion um die Nullstelle herum gleich bleibt.
In einer Funktionsgleichung könnte das so aussehen:- \(f(x)=x^2\)
- \(f(x)=(x-2)^2\)
Dreifache Nullstellen
Eine dreifache Nullstelle ist eine Nullstelle, bei der die Funktion die x-Achse flach schneidet - in einem Sattelpunkt. Das bedeutet auch, dass das Vorzeichen der Funktion um die Nullstelle herum wechselt.
In einer Funktionsgleichung könnte das so aussehen:- \(f(x)=x^3\)
- \(f(x)=(x-2)^3\)
- einfache Nullstelle \(x\) oder \((x-x_0)\)
- doppelte Nullstelle \(x^2\) oder \((x-x_0)^2\)
- dreifache Nullstelle \(x^3\) oder \((x-x_0)^3\)
Ob eine Nullstelle einfach, doppelt oder dreifach ist, siehst du mit deinem Tutor bald auf einen Blick.
Kostenlos testen: Nachhilfe Mathe online bei OnMathe
Vielfachheit von Nullstellen erkennen
- Nullstellen ablesen: Setze jede Klammer gleich Null
- Vielfachheit: Exponent definiert die Art der Nullstelle
- Die faktorisierte Form nennt man auch Nullstellenform
Vom Graph zur Funktionsgleichung
Das ermöglicht es uns, auch umgekehrt alle Nullstellen vom Graphen abzulesen und so die Funktionsgleichung zu bestimmen.
Um den Streckfaktor zu bestimmen, wählen wir einen gut ablesbaren Punkt auf der Funktion und setzen ihn in die Funktionsgleichung ein.
- x-Werte der Nullstellen am Graphen ablesen
- Vielfachheit der Nullstellen dazu notieren
- Für jede Nullstelle den Linearfaktor aufstellen
- Zu einer Funktionsgleichung zusammensetzen, dabei den Streckfaktor a berücksichtigen
- Gut ablesbaren Punkt wählen und in die Funktionsgleichung einsetzen
- Streckfaktor a bestimmen
- Fertige Funktionsgleichung notieren
Vom Graphen zur Gleichung biegt man leicht falsch ab. Mit deinem Tutor kommst du sicher an.
Kostenlos testen: Mathe online lernen mit Nachhilfe von OnMathe
Zusammenfassung
- \(f(x)=2x^{\textcolor{orange}{3}}-4\)
- einfache Nullstelle, Schnittpunkt: \(x \ \textsf{oder} \ (x-x_0)\)
- doppelte Nullstelle, Berührpunkt: \(x^2 \ \textsf{oder} \ (x-x_0)^2 \)
- dreifache Nullstelle, Sattelpunkt: \(x^3 \ \textsf{oder} \ (x-x_0)^3\)
Nullstellen machen Druck? Wir bringen Struktur.
Mathe macht Druck? Wir bringen Struktur.
Dein fester Tutor erklärt dir Nullstellen und Vielfachheit am Graphen.
Mathe-Nachhilfe online mit festem Tutor und Crashkurs vor jedem Test.
Ausgewählt für Dich
Empfohlene Beiträge
Mehr dazu
in unseren FAQs
Was sind Nullstellen einer Funktion?
Nullstellen sind die x-Werte, an denen eine Funktion den Wert 0 annimmt. Graphisch betrachtet sind es die Punkte, an denen der Funktionsgraph die x-Achse schneidet oder berührt.
Welche Arten von Nullstellen gibt es?
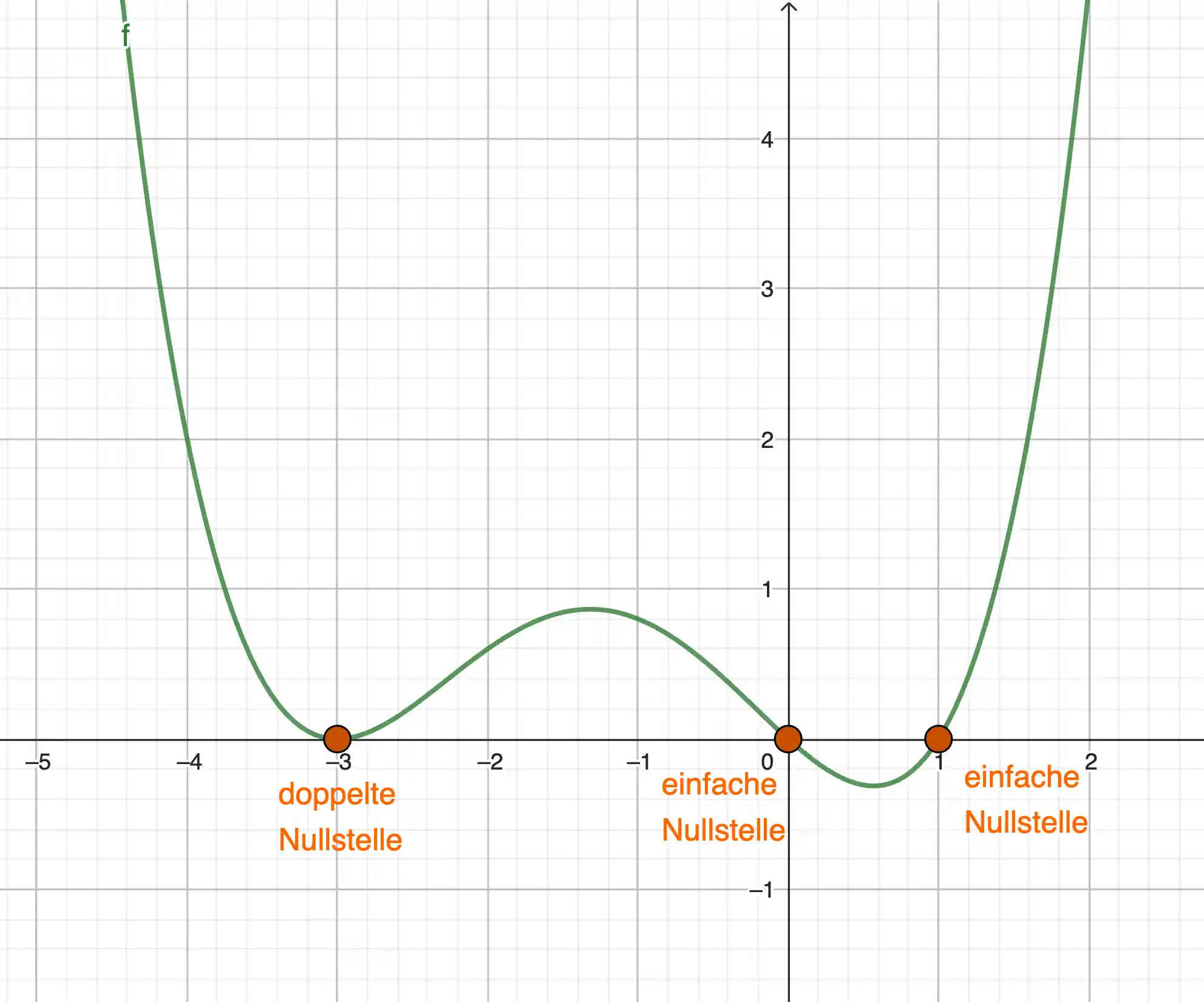
Es gibt einfache Nullstellen, mehrfache Nullstellen und Berührstellen. Eine einfache Nullstelle schneidet die x-Achse, während eine doppelte oder mehrfache Nullstelle den Graphen entweder berühren oder mit einer Flachstelle kreuzen kann.
Was bedeutet die Vielfachheit einer Nullstelle?
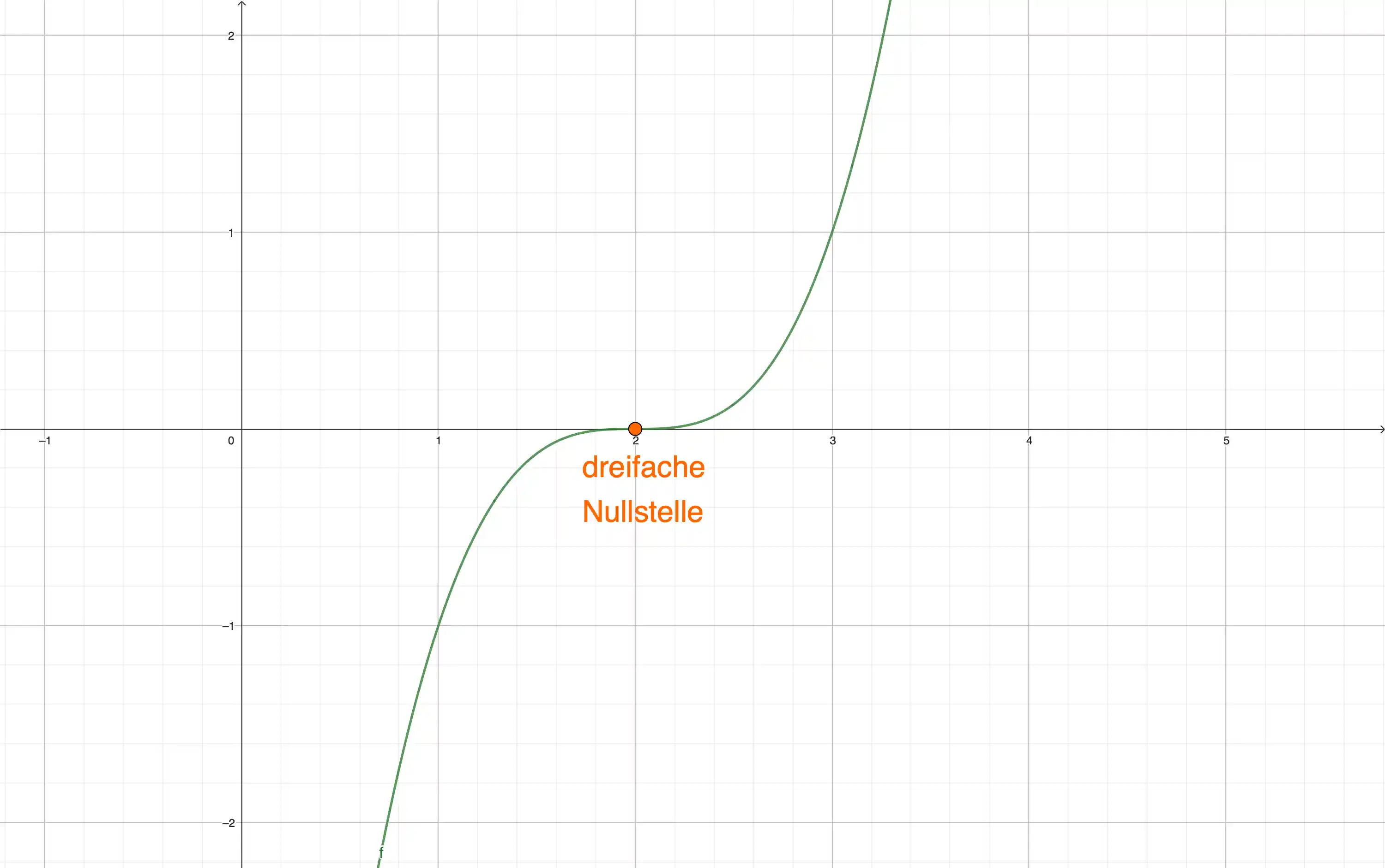
Die Vielfachheit gibt an, wie oft eine Nullstelle in der Funktionsgleichung vorkommt. Eine Vielfachheit von 1 bedeutet, dass der Graph die x-Achse einfach schneidet. Eine Vielfachheit von 2 oder höher bedeutet, dass der Graph die x-Achse berührt oder mit einer Wellenbewegung kreuzt.
Wie erkennt man die Vielfachheit einer Nullstelle in der Funktionsgleichung?
Die Vielfachheit einer Nullstelle erkennt man an der Hochzahl der entsprechenden Klammer in der faktoriellen Darstellung einer Funktion. Wenn eine Klammer beispielsweise eine Hochzahl von 3 hat, bedeutet das, dass die Nullstelle dreifach vorkommt. Eine Hochzahl von 1 steht für eine einfache Nullstelle, eine Hochzahl von 2 für eine doppelte Nullstelle und so weiter.
Warum ist die Vielfachheit von Nullstellen wichtig?
Die Vielfachheit bestimmt, wie sich der Graph an einer Nullstelle verhält. Sie beeinflusst die Steigung des Graphen und entscheidet, ob die Funktion die x-Achse schneidet, berührt oder sich an ihr windet. Dies ist besonders wichtig in der Analysis, um das Verhalten einer Funktion zu verstehen.
Mehr dazu
Weiterführende Informationen
Nullstellen bestimmen – Grundlagen und Bedeutung
Das Nullstellen bestimmen ist eine zentrale Fähigkeit in der Mathematik, die dir hilft, die Punkte zu finden, an denen eine Funktion den Wert Null annimmt. Diese Punkte sind wichtig, um das Verhalten von Funktionen zu verstehen und ihre Graphen korrekt zu zeichnen. Beim Nullstellen bestimmen spielt die Vielfachheit eine entscheidende Rolle, da sie beeinflusst, wie sich der Graph an den Nullstellen verhält. In diesem Beitrag erfährst du, welche Arten von Nullstellen es gibt und wie du sie richtig bestimmst.
Was bedeutet Vielfachheit beim Nullstellen bestimmen?
Beim Nullstellen bestimmen kann eine Funktion nicht nur einfache Nullstellen haben, sondern auch doppelte oder mehrfache Nullstellen. Eine einfache Nullstelle schneidet die x-Achse, während eine doppelte Nullstelle den Graphen nur berührt. Mehrfache Nullstellen sorgen für ein verändertes Krümmungsverhalten der Funktion. Das Nullstellen bestimmen mit Vielfachheit hilft dabei, den Funktionsgraphen präzise zu analysieren.
Wie bestimmt man die Nullstellen einer Funktion?
Beim Nullstellen bestimmen gibt es verschiedene Methoden, die je nach Funktionstyp eingesetzt werden. Während einfache Nullstellen durch direktes Lösen einer Gleichung gefunden werden, können mehrfache Nullstellen durch Faktorisieren oder Ableitungen genauer untersucht werden. Das richtige Vorgehen beim Nullstellen bestimmen ermöglicht eine korrekte Interpretation des Funktionsverlaufs.
Häufige Fehler beim Nullstellen bestimmen
Ein häufiger Fehler beim Nullstellen bestimmen ist das Übersehen der Vielfachheit einer Nullstelle. Wird eine Nullstelle nur einmal berücksichtigt, obwohl sie mehrfach vorkommt, kann dies zu falschen Interpretationen des Graphen führen. Ein weiterer Fehler ist das falsche Anwenden von Rechenmethoden, insbesondere beim Ausklammern oder bei der Anwendung von Wurzelgesetzen. Sorgfältiges Überprüfen hilft, Fehler beim Nullstellen bestimmen zu vermeiden.
Nullstellen bestimmen in der modernen Mathematik
Das Nullstellen bestimmen ist nicht nur eine schulische Übung, sondern spielt auch eine große Rolle in der modernen Mathematik und Wissenschaft. In der Physik werden Nullstellen genutzt, um Gleichgewichtspunkte zu finden, in der Wirtschaftsmathematik helfen sie, Gewinn- und Verlustgrenzen zu bestimmen, und in der Informatik werden sie zur Lösung komplexer Algorithmen verwendet. Das Nullstellen bestimmen bleibt daher eine essenzielle Fähigkeit für viele mathematische und technische Anwendungen.
