Stochastik verstehen
Kombination - wie viele Anordnungen?
Einleitung
Die Kombination beschreibt, wie viele verschiedene Auswahlmöglichkeiten es gibt, wenn nur einige Objekte aus einer Menge gewählt werden und ihre Reihenfolge keine Rolle spielt. → Bei der Kombination werden nur k Elemente aus n ausgewählt.
Wie viele Möglichkeiten gibt es, 3 Schüler aus einer Klasse zu wählen, 5 Karten aus einem Kartenspiel zu ziehen oder ein Team aus mehreren Personen zu bilden? Solche Fragen gehören zur Kombination – dem Teil der Kombinatorik, bei dem nicht die Reihenfolge, sondern nur die Auswahl selbst wichtig ist.
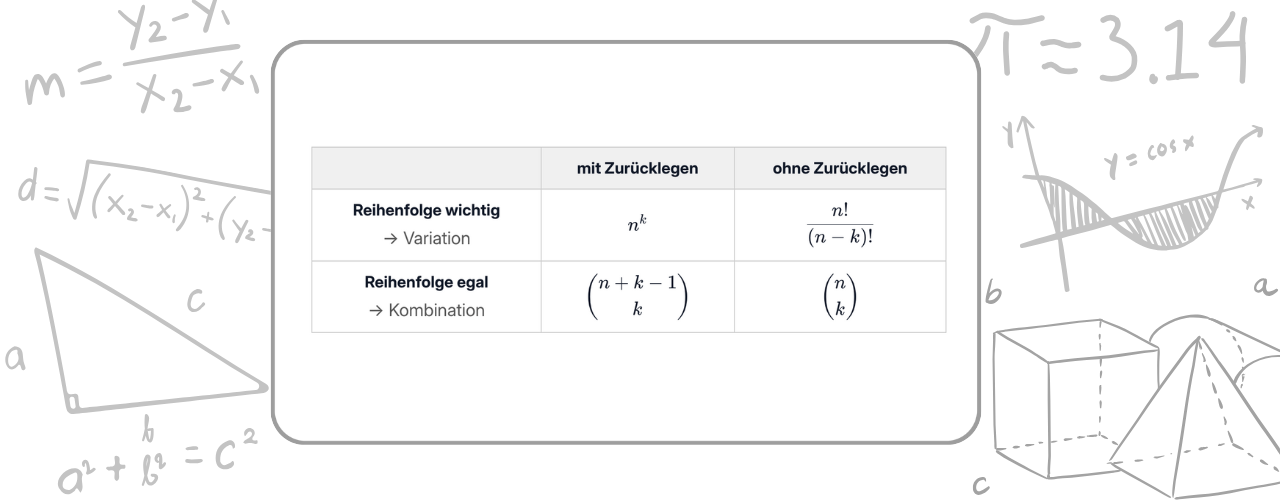
Je nach Situation kann es sein, dass Auswahl mit oder ohne Zurücklegen erfolgt. Manchmal darf ein Objekt also mehrfach vorkommen, manchmal nur einmal. Daraus ergeben sich zwei Arten der Kombination.
Überblick: Die beiden Arten der Kombination
| Art | Formel | Wann? |
|---|---|---|
| Kombination ohne Wiederholung | \( \displaystyle \binom{{\textcolor{orange}{n}}}{{\textcolor{green}{k}}} = \dfrac{{\textcolor{orange}{n}}!}{({\textcolor{orange}{n}} - {\textcolor{green}{k}})! \cdot {\textcolor{green}{k}}!} \) | Jedes Objekt kann nur einmal gewählt werden. |
| Kombination mit Wiederholung | \( \displaystyle \binom{{\textcolor{orange}{n}} + {\textcolor{green}{k}} - 1}{{\textcolor{green}{k}}} = \dfrac{({\textcolor{orange}{n}} + {\textcolor{green}{k}} - 1)!}{({\textcolor{orange}{n}} - 1)! \cdot {\textcolor{green}{k}}!} \) | Objekte dürfen mehrfach gewählt werden. |
In den nächsten Abschnitten schauen wir uns beide Arten genauer an: zuerst die Kombination ohne Wiederholung – also wenn jedes Objekt nur einmal gewählt werden darf – und danach die Kombination mit Wiederholung, bei der Objekte auch mehrfach vorkommen können.
Einleitung
Die Kombination beschreibt, wie viele verschiedene Auswahlmöglichkeiten es gibt, wenn nur einige Objekte aus einer Menge gewählt werden und ihre Reihenfolge keine Rolle spielt. → Bei der Kombination werden nur k Elemente aus n ausgewählt.
Wie viele Möglichkeiten gibt es, 3 Schüler aus einer Klasse zu wählen, 5 Karten aus einem Kartenspiel zu ziehen oder ein Team aus mehreren Personen zu bilden? Solche Fragen gehören zur Kombination – dem Teil der Kombinatorik, bei dem nicht die Reihenfolge, sondern nur die Auswahl selbst wichtig ist.
Je nach Situation kann es sein, dass Auswahl mit oder ohne Zurücklegen erfolgt. Manchmal darf ein Objekt also mehrfach vorkommen, manchmal nur einmal. Daraus ergeben sich zwei Arten der Kombination.
Überblick: Die beiden Arten der Kombination
| Art | Formel | Wann? |
|---|---|---|
| Kombination ohne Wiederholung | \( \displaystyle \binom{{\textcolor{orange}{n}}}{{\textcolor{green}{k}}} = \dfrac{{\textcolor{orange}{n}}!}{({\textcolor{orange}{n}} - {\textcolor{green}{k}})! \cdot {\textcolor{green}{k}}!} \) | Jedes Objekt kann nur einmal gewählt werden. |
| Kombination mit Wiederholung | \( \displaystyle \binom{{\textcolor{orange}{n}} + {\textcolor{green}{k}} - 1}{{\textcolor{green}{k}}} = \dfrac{({\textcolor{orange}{n}} + {\textcolor{green}{k}} - 1)!}{({\textcolor{orange}{n}} - 1)! \cdot {\textcolor{green}{k}}!} \) | Objekte dürfen mehrfach gewählt werden. |
In den nächsten Abschnitten schauen wir uns beide Arten genauer an: zuerst die Kombination ohne Wiederholung – also wenn jedes Objekt nur einmal gewählt werden darf – und danach die Kombination mit Wiederholung, bei der Objekte auch mehrfach vorkommen können.
Kombination ohne Wiederholung
Bei einer Kombination ohne Wiederholung wählst du k Elemente aus einer Menge von n unterschiedlichen Objekten aus. Die Reihenfolge ist egal und jedes Objekt darf höchstens einmal vorkommen. Wir zählen also nur, welche Objekte ausgewählt werden – nicht, in welcher Reihenfolge.
Typische Beispiele: Teams zusammenstellen, Kartenhand wählen, Farbkombinationen bestimmen – immer dann, wenn die Reihenfolge keine Rolle spielt.
Du ziehst dreimal hintereinander jeweils eine Kugel, ohne Zurücklegen.
Jetzt ist dir die Reihenfolge egal.
Frage: Wie viele unterschiedliche Kombinationen aus 3 Kugeln gibt es?
Die Reihenfolge ist hier nicht wichtig, das bedeutet:
Die Abfolgen blau–gelb–rot, rot–gelb–blau und gelb–rot–blau
zählen alle als eine einzige Kombination,
weil sie aus denselben drei Farben bestehen.
- 3 Kugeln werden aus 5 Kugeln gezogen
- die Kugeln werden nicht zurückgelegt
- es zählt nur, welche Farben am Ende dabei sind
- die Reihenfolge spielt keine Rolle
Das hier ist die Situation: ohne Zurücklegen und Reihenfolge egal.
Die passende Formel dazu ist der sogenannte Binomialkoeffizient:
Der Binomialkoeffizient beschreibt, wie viele verschiedene Möglichkeiten es gibt, aus \( {\textcolor{orange}{n}} \) Objekten genau \( {\textcolor{green}{k}} \) auszuwählen – ohne dass die Reihenfolge eine Rolle spielt.
Man liest ihn „n über k“ und schreibt ihn als \( \displaystyle \binom{{\textcolor{orange}{n}}}{{\textcolor{green}{k}}} \). Diese Schreibweise brauchst du später wieder bei der Binomialverteilung insbesondere für die Bernoulli-Formel.
In unserem Beispiel bedeutet das: Wir wählen \( {\textcolor{green}{k}} = {\textcolor{green}{3}} \) Kugeln aus \( {\textcolor{orange}{n}} = {\textcolor{orange}{5}} \) ohne Zurücklegen und ohne Reihenfolge.
Woher kommt diese 10? Ganz einfach: Entweder du nimmst direkt die nCr-Taste am Taschenrechner, oder du rechnest die Formel selbst aus.
Wenn du ohne nCr-Taste rechnest, brauchst du die Formel:
Schauen wir uns diese Formel jetzt einmal Stück für Stück an.
Oben, im Zähler des Bruchs steht \( {\textcolor{orange}{n}}! \). Bezogen auf unser Beispiel heißt das:
Haben wir nicht gelernt, dass die Fakultät auch die Reihenfolge der Objekte betrachtet? Aber genau das wollen wir hier nicht – die Reihenfolge spielt ja keine Rolle.
Und jetzt kommt der Nenner ins Spiel.
Er besteht aus zwei Teilen:
\( {\textcolor{green}{k}}! \) und \( ({\textcolor{orange}{n}}-{\textcolor{green}{k}})! \)
Stell dir unsere Kugeln als Kuchenstücke an einer Theke vor. Du darfst dir 3 Stücke aussuchen – aber egal, in welcher Reihenfolge du sie nimmst: Du hast am Ende dieselben 3 Stücke.
Für jede Auswahl gibt es also immer mehrere Möglichkeiten, in welcher Reihenfolge wir sie wählen könnten. Das gilt auch für unsere Kugeln – jede Kombination aus drei Kugeln kann in mehreren Reihenfolgen gezogen werden.
Und wie wir schon bei der Permutation gelernt haben, bestimmt man die Anzahl aller möglichen Reihenfolgen mit der Fakultät der entsprechenden Anzahl an Objekten.
Das heißt: Für jede Auswahl aus \( {\textcolor{green}{3}} \) Kugeln gibt es mehrere Reihenfolgen, in denen wir sie hätten ziehen können – nämlich \( {\textcolor{green}{3}}! \).
Fehlt nur noch der zweite Teil des Nenners: \( ({\textcolor{orange}{n}}-{\textcolor{green}{k}})! \).
Diesen Ausdruck brauchen wir immer dann, wenn ein Teil der Objekte nicht ausgewählt wird. Er steht also für die übrig gebliebenen Elemente. In unserem Beispiel bleiben nach den 3 gezogenen Kugeln noch 2 Kugeln übrig, die wir nicht mehr berücksichtigen. Vielleicht kommt dir dieser Ausdruck bekannt vor – wir verwenden ihn auch bei der Variation ohne Wiederholung.
Auch diese übrigen Kugeln könnten theoretisch noch vertauscht werden, obwohl sie für unsere Auswahl keine Rolle spielen. Diese überflüssigen Vertauschungen kürzen wir mit \( ({\textcolor{orange}{n}}-{\textcolor{green}{k}})! \) heraus.
Damit haben wir jetzt den gesamten Nenner:
Und damit auch die komplette Formel für die Kombination ohne Zurücklegen:
Jetzt fassen wir alles zusammen und wenden die Formel auf unser Beispiel an: Wir wählen \( {\textcolor{green}{k}} = {\textcolor{green}{3}} \) Kugeln aus einer Gesamtmenge von \( {\textcolor{orange}{n}} = {\textcolor{orange}{5}} \). Diese Werte setzen wir nun in die allgemeine Formel ein.
Wir setzen die Werte jetzt in die Formel ein:
Das kannst du mit dem Taschenrechner berechnen, oder aber du nutzt die ausführliche Formel:
Wir setzen die Fakultäten Schritt für Schritt ein:
Das bedeutet: Es gibt 10 verschiedene Kombinationen, die aus 3 Kugeln einer Menge von 5 Kugeln gebildet werden können – ohne Zurücklegen und ohne Beachtung der Reihenfolge.
- Mit der nCr-Taste:
- Mit der ausführlichen Formel
Wir wählen \( {\textcolor{green}{k}} = {\textcolor{green}{5}} \) Schüler aus \( {\textcolor{orange}{n}} = {\textcolor{orange}{20}} \). Die Reihenfolge spielt keine Rolle, es soll einfach nur jede mögliche Gruppe aus 5 verschiedenen Personen gezählt werden.
- ohne Zurücklegen (Es gibt jede Person nur einmal)
- Reihenfolge egal (Egal wie gewählt wird, das Team bleibt das Gleiche)
- gesucht: Anzahl verschiedener 5er-Teams aus 20 Personen
Formel wählen: Kombination ohne Wiederholung → Binomialkoeffizient.
Gegeben:
Einsetzen der Werte:
Ergebnis: Es gibt 15 504 verschiedene Gruppen, die aus 20 Schülern zu je 5 Personen gebildet werden können.
Taschenrechner: \( {\textcolor{orange}{20}} \rightarrow \textsf{nCr} \rightarrow {\textcolor{green}{5}} = {\textcolor{midnightblue}{15504}} \).
Antwort: Es gibt 15 504 verschiedene Gruppen, die aus 20 Schülern zu je 5 Personen gebildet werden können.
Kombination mit Wiederholung
Bei der Kombination mit Zurücklegen wählst du aus einer Gesamtmenge von Objekten mehrere Elemente aus, wobei jedes Objekt mehrfach vorkommen darf. Die Reihenfolge spielt keine Rolle – entscheidend ist nur, welche Objekte am Ende ausgewählt wurden. Das unterscheidet sie von der Variation, bei der die Reihenfolge wichtig ist.
Man kann sich das so vorstellen: Du darfst bei jedem Zug aus derselben Menge wählen, denn jedes gezogene Objekt wird wieder zurückgelegt. Damit sind mehrfache Wiederholungen erlaubt, aber wir zählen nur die Kombinationen der Auswahl, nicht die Reihenfolgen.
Wie viele unterschiedliche Kombinationen sind möglich?
Wir haben hier eine Kombination mit Zurücklegen → Die Reihenfolge ist uns egal.
- es werden 3 Kugeln aus 4 Farben gezogen
- nach jedem Zug wird die Kugel wieder zurückgelegt
- bei jedem Zug liegen alle 4 Farben in der Kiste
- es kann vorkommen, dass eine Farbe mehrmals gezogen wird
- die Reihenfolge spielt keine Rolle – nur die gezogenen Farben zählen
Wir wollen also herausfinden, wie viele Möglichkeiten es gibt, aus n verschiedenen Farben k-mal zu ziehen – und das, obwohl sich Farben auch wiederholen dürfen. Dafür nutzen wir wieder den Binomialkoeffizienten, diesmal aber in einer etwas angepassten Version:
Diese Schreibweise liest man „n + k − 1 über k“. Der Ausdruck \( {\textcolor{orange}{n}} + {\textcolor{green}{k}} - 1 \) wirkt zunächst ungewohnt, zeigt aber, dass sich Farben wiederholen dürfen und wir deshalb nicht nur entscheiden, welche Objekte wir nehmen, sondern auch wann und wie oft wir die Sorte wechseln. Wir stellen uns das einmal bildlich vor.
Du stehst vor einem Kuchenbuffet: Es gibt \( {\textcolor{orange}{n}} = {\textcolor{orange}{4}} \) verschiedene Sorten – Apfel, Schoko, Erdbeer und Zitrone. Du darfst dir \( {\textcolor{green}{k}} = {\textcolor{green}{3}} \) Stücke aussuchen.
Und weil dir niemand vorschreibt, was du essen sollst, kannst du dieselbe Sorte auch mehrmals wählen.
Wichtig ist: Am Ende zählt nur, welche Sorten du gewählt hast – nicht, in welcher Reihenfolge du sie bestellt hast. Ob du erst Apfel, dann Schoko und danach Erdbeer nimmst oder mit Schoko anfängst und Apfel zuletzt wählst – am Ende liegen dieselben drei Stücke auf deinem Teller. Und niemand hindert dich daran, dieselbe Sorte auch mehrfach zu wählen.
Ergebnis: 3 Stücke, aber nur 2 Sorten.
Wenn in der Kuchentheke \( {\textcolor{orange}{4}} \) verschiedene Sorten stehen, könntest du – wenn wir alle Wahlmöglichkeiten betrachten – \( {\textcolor{green}{3}} \)-mal die Sorte wechseln. Nach jedem Stück könntest du eine neue Sorte wählen. Ich kann also immer einmal weniger die Sorte wechseln, als ich Sorten vor mir habe.
Außerdem haben wir auf unserem Teller Platz für 3 Stücke Kuchen. Das ist der zweite Aspekt, der in unsere Überlegung mit einfließt.
Für unsere Rechnung sind also zwei Dinge wichtig:
Diese beiden Aspekte führen uns nun direkt zur Formel \( {\textcolor{orange}{n}} + {\textcolor{green}{k}} - 1 \). Das \( {\textcolor{orange}{n}} - 1 \) steht für die möglichen Sortenwechsel, und das \( {\textcolor{green}{k}} \) für die tatsächlich gewählten Objekte. Nur wenn wir beides zusammennehmen wissen wir, wie viele Auswahlmöglichkeiten insgesamt entstehen, wenn wir uns auch immer wieder für dieselbe Sorte entscheiden dürften, aber die Reihenfolge keine Rolle spielt.
Jetzt fehlt noch der untere Teil: das \( {\textcolor{green}{k}} \).
Das \( {\textcolor{green}{k}} \) steht – wie gewohnt – für die vorgegebene Anzahl der Objekte, die wir auswählen. Mit diesem Wissen gehen wir wieder zurück zu unserem Beispiel mit den \( {\textcolor{green}{3}} \) Kugeln, die wir wählen wollen.
Wir haben also \( {\textcolor{orange}{n}} = {\textcolor{orange}{4}} \) Farben und \( {\textcolor{green}{k}} = {\textcolor{green}{3}} \) Kugeln → Kombination mit Zurücklegen.
Es gibt also 20 verschiedene Möglichkeiten, wie du \( {\textcolor{green}{3}} \) Kugeln aus \( {\textcolor{orange}{4}} \) Farben ziehen kannst – auch wenn dieselbe Farbe mehrfach vorkommt.
Und wenn du keinen Taschenrechner mit nCr-Funktion hast, kannst du das Ergebnis auch wieder mit der Formel berechnen.
Diese Variante kennst du bereits aus dem vorherigen Abschnitt.
Der Unterschied liegt nur im Zähler:
statt \( {\textcolor{orange}{n}}! \) steht hier \( ({\textcolor{orange}{n}} + {\textcolor{green}{k}} - 1)! \).
Wir setzen diese Werte jetzt in die Formel ein:
Zuerst berechnen wir den oberen Ausdruck \( {\textcolor{orange}{n}} + {\textcolor{green}{k}} - 1 \):
Damit erhalten wir den Binomialkoeffizienten:
Nun setzen wir die Fakultäten ein:
Ergebnis: Es gibt 20 verschiedene Kombinationen, in denen du \( {\textcolor{green}{3}} \) Kugeln aus \( {\textcolor{orange}{4}} \) Farben ziehen kannst – auch wenn dieselbe Farbe mehrfach vorkommt.
- \( {\textcolor{orange}{n}} \): Anzahl der verschiedenen Objekte (Farben, Sorten …)
- \( {\textcolor{green}{k}} \): Anzahl der gewählten Objekte (gezogene Kugeln …)
Wir wählen \( {\textcolor{green}{k}} = {\textcolor{green}{4}} \) Brötchen aus \( {\textcolor{orange}{n}} = {\textcolor{orange}{5}} \) Sorten, wobei dieselbe Sorte mehrfach genommen werden darf → mit Zurücklegen.
Wir setzen also wieder in die Formel ein:
Antwort: Es gibt 70 verschiedene Möglichkeiten, \( {\textcolor{green}{4}} \) Brötchen aus \( {\textcolor{orange}{5}} \) Sorten zu wählen – auch wenn du dieselbe Sorte mehrfach nimmst.
Du siehst also: Kombination mit Zurücklegen bedeutet, dass Wiederholungen erlaubt sind, aber die Reihenfolge egal ist. Deshalb wird sie auch oft als „Auswahl mit Mehrfachnennungen“ bezeichnet.
Mit oder ohne Wiederholung, was bedeutet das?
Mit oder ohne Wiederholung – was bedeutet das?
Auch bei Kombinationen gibt es zwei Varianten: mit und ohne Wiederholung. Aber was genau unterscheidet sie?
Der Unterschied liegt darin, ob ein Objekt mehrfach gewählt werden darf oder nicht. Das entscheidet darüber, wie viele verschiedene Auswahlmöglichkeiten entstehen.
| ohne Wiederholung | mit Wiederholung | |
|---|---|---|
| Bedeutung | Jedes Objekt kann nur einmal gewählt werden. | Ein Objekt darf mehrmals gewählt werden. |
| Beispiel | Du ziehst 3 Kugeln aus einer Kiste mit 5 Farben → jede Kugel nur einmal. | Du darfst mehrmals dieselbe Farbe ziehen → Kugeln werden zurückgelegt. |
| Formel (kurz) | \( \displaystyle \binom{{\textcolor{orange}{n}}}{{\textcolor{green}{k}}} \) | \( \displaystyle \binom{{\textcolor{orange}{n}}+{\textcolor{green}{k}}-1}{{\textcolor{green}{k}}} \) |
| Typischer Gedanke | „Ich wähle jedes Objekt nur einmal aus.“ | „Ich darf dieselbe Sorte oder Farbe mehrmals wählen.“ |
Die ausführlichen Formeln sehen so aus:
Kurz gesagt: Bei der Kombination ohne Wiederholung wird jedes Objekt nur einmal gewählt. Bei der Kombination mit Wiederholung dürfen sich Objekte wiederholen – die Reihenfolge bleibt trotzdem egal.
Abschlussbeispiele
Zum Schluss zwei typische Aufgaben – eine ohne Wiederholung und eine mit Wiederholung. Wichtig ist zuerst das Herausfiltern der Größen aus dem Text: Was ist die Gesamtzahl aller Objekte \( {\textcolor{orange}{n}} \)? Wie viele werden ausgewählt \( {\textcolor{green}{k}} \)? Und: Dürfen sich Objekte wiederholen?
Beispiel 1: Schüler für ein Team (ohne Wiederholung)
Text → Größen filtern
- Wir wählen nur einen Teil aus → Kombination.
- Niemand wird doppelt gewählt → ohne Wiederholung.
- Reihenfolge egal → Kombination ohne Wiederholung.
- \( {\textcolor{orange}{n}} = 12 \), \( {\textcolor{green}{k}} = 3 \)
Formel wählen:
Wenn wir aus einer Menge n Objekte auswählen und die Reihenfolge keine Rolle spielt, nutzen wir den Binomialkoeffizienten:
Einsetzen der Werte:
Taschenrechner: \( {\textcolor{orange}{12}} \rightarrow \textsf{nCr} \rightarrow {\textcolor{green}{3}} = {\textcolor{midnightblue}{220}} \)
Antwort: 220 verschiedene Teams.
Beispiel 2: Eistüten zusammenstellen (mit Wiederholung)
Text → Größen filtern
- Auswahl aus mehreren Sorten → Kombination.
- Wiederholungen erlaubt → mit Zurücklegen.
- Reihenfolge egal → Kombination mit Wiederholung.
- \( {\textcolor{orange}{n}} = 5 \), \( {\textcolor{green}{k}} = 3 \)
Formel wählen:
Wiederholungen sind erlaubt → wir passen den Binomialkoeffizienten an:
Einsetzen der Werte:
Taschenrechner: \( {\textcolor{midnightblue}{7}} \rightarrow \textsf{nCr} \rightarrow {\textcolor{green}{3}} = {\textcolor{midnightblue}{35}} \)
Antwort: 35 verschiedene Eistüten mit drei Kugeln aus fünf Sorten.
Du suchst Profi-Nachhilfe mit echtem Impact? Dann bist du bei OnMathe genau richtig!
Verstehe Mathe ab der ersten Stunde - 1:1 Online-Nachhilfe von echten Profis.

Teste dein Wissen
Übungen
Lösung
Lösung
Ausgewählt für Dich
Empfohlene Beiträge
Mehr dazu
in unseren FAQs
1. Was ist der Unterschied zwischen Kombination und Variation?
Bei der Kombination zählt nur, welche Objekte du auswählst.
Bei der Variation zählt auch die Reihenfolge.
→ Kombination = Auswahl
→ Variation = Reihenfolge wichtig
2. Woran erkenne ich, ob mit oder ohne Wiederholung gerechnet wird?
Immer im Text schauen:
Wenn ein Objekt nur einmal vorkommen darf → ohne Wiederholung.
Wenn ein Objekt mehrmals erlaubt ist → mit Wiederholung.
3. Wann benutze ich „n über k“?
Immer dann, wenn du aus einer Menge nur einige Objekte auswählst und die Reihenfolge egal ist.
Egal ob mit oder ohne Wiederholung – das Grundprinzip bleibt: Reihenfolge spielt keine Rolle.
4. Kann ich die Kombination immer mit der nCr-Taste berechnen?
Ja!
Die nCr-Taste am Taschenrechner ist genau dafür da, die Anzahl der Kombinationen zu bestimmen.
Du gibst zuerst n, dann nCr, dann k ein.
5. Woher weiß ich, welche Werte n und k sind?
Das steht immer im Text:
- n = wie viele Objekte es insgesamt gibt
- k = wie viele davon ausgewählt werden
- Erst diese beiden bestimmen, welche Formel du brauchst.
Vertiefung
Weiterführende Informationen
Kombination Formeln als Werkzeug in der Mathematik
Die Kombination Formeln helfen dir herauszufinden, wie viele verschiedene Auswahlen möglich sind, wenn nur ein Teil einer Menge gewählt wird. Sie sind ein wichtiges Werkzeug, wenn du berechnen willst, wie viele Gruppen, Teams oder Zusammenstellungen man bilden kann, ohne die Reihenfolge zu beachten. Mit den Kombination Formeln erkennst du schnell, welche Auswahlmöglichkeiten entstehen – egal ob mit oder ohne Wiederholung.
Was sind Kombination Formeln?
Kombination Formeln beschreiben mathematisch, wie groß die Anzahl aller möglichen Zusammenstellungen ist. Dabei geht es immer um die Frage, wie viele Elemente ausgewählt werden und ob ein Element mehrfach vorkommen darf. Die Kombination Formeln unterscheiden deshalb klar zwischen Auswahl ohne Wiederholung und Auswahl mit Wiederholung. In beiden Fällen zählt nur der Inhalt der Auswahl, nicht die Reihenfolge.
Mathematische Bedeutung
Die Kombination Formeln sind ein zentraler Bestandteil der Kombinatorik und bilden später die Grundlage für viele Themen in der Wahrscheinlichkeit, zum Beispiel bei der Binomialverteilung oder der Bernoulli-Formel. Sie beschreiben Auswahlen aus einer Menge und zeigen dir, wie groß die Anzahl der möglichen Zusammenstellungen ist. Damit helfen die Kombination Formeln, komplexe Fragestellungen verständlich und systematisch zu lösen.
Typische Fehler & wie du sie vermeidest
Ein häufiger Fehler besteht darin, die Kombination Formeln mit den Formeln der Variation zu verwechseln. Viele verwechseln, ob die Reihenfolge eine Rolle spielt oder ob man dieselben Elemente mehrfach wählen darf. Oft wird auch vergessen, zuerst n und k sauber aus dem Text zu bestimmen. Achte außerdem darauf, ob ein Objekt mehrmals vorkommen darf – das entscheidet darüber, welche Kombination Formel du brauchst. Überprüfe zum Schluss immer, ob du die Auswahl wirklich ohne Reihenfolge betrachtest.
Lerntipps für Kombination Formeln
Lies jede Aufgabe zuerst langsam und markiere die entscheidenden Wörter: „ohne Zurücklegen“, „mit Zurücklegen“, „Reihenfolge egal“. Ordne sie dann sofort einer der beiden Kombination Formeln zu. Übe außerdem kleine Beispiele im Kopf, um ein Gefühl dafür zu bekommen, wann Wiederholungen erlaubt sind. Wenn du dir unsicher bist, stell dir eine reale Situation vor, etwa Kugeln ziehen oder Gruppen einteilen.
Ursprung und Entwicklung
Die Kombination Formeln stammen aus der klassischen Kombinatorik, einem Gebiet, das sich schon sehr früh damit beschäftigt hat, wie man Dinge zählt, ohne alles einzeln aufschreiben zu müssen. Die Idee, Auswahlen zu zählen, ohne die Reihenfolge zu beachten, entwickelte sich aus praktischen Problemen wie Wahlmöglichkeiten, Kartenkombinationen oder mathematischen Spielen. Mit der Zeit wurden die Kombination Formeln präziser gefasst und sind heute ein fester Bestandteil der Algebra und Wahrscheinlichkeitsrechnung.
Moderne Anwendung
Heute begegnen dir die Kombination Formeln in vielen Bereichen, oft ohne dass man sie direkt erkennt. In der Statistik, im Machine Learning, bei genetischen Kombinationen, in der Informatik oder bei Auswertungen großer Datenmengen werden Kombination Formeln ständig verwendet. Auch bei Kartenspielen, Losziehungen oder Teamzusammenstellungen sind sie unverzichtbar. Die Kombination Formeln zeigen dir, wie viele Möglichkeiten es gibt – und genau diese Idee brauchst du in vielen modernen Problemlösungen.

13:00 -18:30 Uhr
5 von 5 Sternen auf Google