Binomialverteilte Zufallsgrößen

Die Binomialverteilung – mit Formel & Beispielen

Lisa von OnMathe
two students high five

Einleitung

Die Binomialverteilung ist die Übersicht aller Wahrscheinlichkeiten für die möglichen Trefferzahlen einer Bernoulli-Kette.

Ein Spieler trifft mit \( {\textcolor{green}{p = 0{,}6}} \) und wirft \( {\textcolor{orange}{n = 8}} \)-mal.
Dabei sind verschiedene Trefferzahlen möglich:
\( {\textcolor{blue}{k}} = 0, 1, 2, 3, 4, 5, 6, 7, 8 \)
Für jede dieser Trefferzahlen gibt es eine eigene Wahrscheinlichkeit.
Alle diese Einzelwahrscheinlichkeiten zusammen bilden die Binomialverteilung.
Stellt man sie als Säulen dar, entsteht ein Histogramm.
In diesem Beitrag lernst du, wie du Aufgaben zur Binomialverteilung mit dem Taschenrechner löst – besonders dann, wenn du „mindestens“, „höchstens“ oder „zwischen“ berechnen sollst.
Merke
Der TR kann nur höchstens rechnen: \( P(X \le k) \)
Typische Umformungen:
\( {\textcolor{orange}{P(X \ge k)}} = 1 - {\textcolor{green}{P(X \le k-1)}} \)
\( {\textcolor{orange}{P(X > k)}} = 1 - {\textcolor{green}{P(X \le k)}} \)
\( {\textcolor{orange}{P(X < k)}} = {\textcolor{green}{P(X \le k-1)}} \)
\( {\textcolor{orange}{P(a \le X \le b)}} = {\textcolor{green}{P(X \le b)}} - {\textcolor{green}{P(X \le a-1)}} \)
Die Binomialverteilung baut auf der Bernoulli-Formel auf. Wenn du erst einmal ein einzelnes Zufallsexperiment verstehen willst, schau dort unbedingt rein.
Wichtig
• Bernoulli-Experiment
→ ein einzelner Versuch mit Treffer / kein Treffer
• Bernoulli-Kette
→ dasselbe Bernoulli-Experiment mehrfach hintereinander
• Binomialverteilung
→ Übersicht aller \( P(X={\textcolor{blue}{k}}) \) für \( {\textcolor{blue}{k}} = 0,1,2,\dots,{\textcolor{orange}{n}} \)
• Kumulierte Wahrscheinlichkeit
→ mehrere Trefferzahlen zusammengefasst
z. B. „höchstens \( {\textcolor{blue}{3}} \) Treffer“

Inhaltsverzeichnis

Das erwartet Dich

Einleitung
Kumulierte Wahrscheinlichkeiten - höchstens
Arbeiten mit dem Taschenrechner
Histogramme erstellen

Einleitung

Die Binomialverteilung ist die Übersicht aller Wahrscheinlichkeiten für die möglichen Trefferzahlen einer Bernoulli-Kette.

Ein Spieler trifft mit \( {\textcolor{green}{p = 0{,}6}} \) und wirft \( {\textcolor{orange}{n = 8}} \)-mal.
Dabei sind verschiedene Trefferzahlen möglich:
\( {\textcolor{blue}{k}} = 0, 1, 2, 3, 4, 5, 6, 7, 8 \)
Für jede dieser Trefferzahlen gibt es eine eigene Wahrscheinlichkeit.
Alle diese Einzelwahrscheinlichkeiten zusammen bilden die Binomialverteilung.
Stellt man sie als Säulen dar, entsteht ein Histogramm.
In diesem Beitrag lernst du, wie du Aufgaben zur Binomialverteilung mit dem Taschenrechner löst – besonders dann, wenn du „mindestens“, „höchstens“ oder „zwischen“ berechnen sollst.
Merke
Der TR kann nur höchstens rechnen: \( P(X \le k) \)
Typische Umformungen:
\( {\textcolor{orange}{P(X \ge k)}} = 1 - {\textcolor{green}{P(X \le k-1)}} \)
\( {\textcolor{orange}{P(X > k)}} = 1 - {\textcolor{green}{P(X \le k)}} \)
\( {\textcolor{orange}{P(X < k)}} = {\textcolor{green}{P(X \le k-1)}} \)
\( {\textcolor{orange}{P(a \le X \le b)}} = {\textcolor{green}{P(X \le b)}} - {\textcolor{green}{P(X \le a-1)}} \)
Die Binomialverteilung baut auf der Bernoulli-Formel auf. Wenn du erst einmal ein einzelnes Zufallsexperiment verstehen willst, schau dort unbedingt rein.
Wichtig
• Bernoulli-Experiment
→ ein einzelner Versuch mit Treffer / kein Treffer
• Bernoulli-Kette
→ dasselbe Bernoulli-Experiment mehrfach hintereinander
• Binomialverteilung
→ Übersicht aller \( P(X={\textcolor{blue}{k}}) \) für \( {\textcolor{blue}{k}} = 0,1,2,\dots,{\textcolor{orange}{n}} \)
• Kumulierte Wahrscheinlichkeit
→ mehrere Trefferzahlen zusammengefasst
z. B. „höchstens \( {\textcolor{blue}{3}} \) Treffer“

Kumulierte Wahrscheinlichkeiten - höchstens

Eine kumulierte Wahrscheinlichkeit fasst mehrere Trefferzahlen in einem Ergebnis zusammen.

Schauen wir uns das direkt an einem Beispiel an.

Du wirfst \( {\textcolor{orange}{10}} \)-mal einen Würfel.
Treffer: jede gewürfelte 5.
Wie wahrscheinlich ist es, höchstens \( {\textcolor{blue}{3}} \) Treffer zu erzielen?

„Höchstens 3“ bedeutet:

  • keine 5 → \( P(X=0) \)
  • genau eine 5 → \( P(X=1) \)
  • genau zwei 5en → \( P(X=2) \)
  • genau drei 5en → \( P(X=3) \)

Diese Einzelwahrscheinlichkeiten können wir mit der Bernoulli-Formel berechnen.

\( \textcolor{orange}{n=10} \quad \textcolor{green}{p=\dfrac{1}{6}} \quad \textcolor{blue}{k=0,1,2,3} \)
\( \displaystyle P(X = {\textcolor{blue}{k}}) = \binom{{\textcolor{orange}{n}}}{{\textcolor{blue}{k}}} \cdot {\textcolor{green}{p}}^{\textcolor{blue}{k}} \cdot (1-{\textcolor{green}{p}})^{{\textcolor{orange}{n}}-{\textcolor{blue}{k}}} \)
Beispielrechnung für \( {\textcolor{blue}{k = 2}} \)
\( \displaystyle P(X = {\textcolor{blue}{2}}) = \binom{{\textcolor{orange}{10}}}{{\textcolor{blue}{2}}} \cdot \left(\dfrac{1}{6}\right)^{\textcolor{blue}{2}} \cdot \left(\dfrac{5}{6}\right)^{{\textcolor{orange}{10}}-{\textcolor{blue}{2}}} \)

So berechnen wir alle Einzelwahrscheinlichkeiten …

\( P(X={\textcolor{blue}{0}}) \approx 0{,}162 \)
\( P(X={\textcolor{blue}{1}}) \approx 0{,}323 \)
\( P(X={\textcolor{blue}{2}}) \approx 0{,}291 \)
\( P(X={\textcolor{blue}{3}}) \approx 0{,}155 \)

… und addieren, um die gesuchte kumulierte Wahrscheinlichkeit zu erhalten.

\( P(X \leq {\textcolor{blue}{3}}) = 0{,}162 + 0{,}323 + 0{,}291 + 0{,}155 \)
\( = \textcolor{midnightblue}{0{,}9302} \)
→ Die Wahrscheinlichkeit für höchstens 3 Treffer beträgt also etwa 93,0 %.
Wichtig
Bei einer kumulierten Wahrscheinlichkeit berechnest du mehrere Einzelwahrscheinlichkeiten (mit der Bernoulli-Formel) und addierst sie.
Merke
„Höchstens \(k\)“ bedeutet:
\( P(0)+P(1)+\dots+P(k) \)
Wichtig
Bei „höchstens \(k\) Treffern“ musst du immer bei 0 starten.
0, 1, 2, …, \(k\)
Die 0 Treffer gehören also immer dazu und dürfen nicht vergessen werden.

Das funktioniert – ist aber bei großen \( {\textcolor{orange}{n}} \) sehr aufwendig.

Deshalb nutzen wir den Taschenrechner, er übernimmt diese Arbeit.

• Er berechnet alle Einzelwahrscheinlichkeiten von \( X=0 \) bis zu einem gewählten \( {\textcolor{blue}{k}} \)
• und addiert sie automatisch

Die Funktion, die wir brauchen ist binomCDF.

Taschenrechner
Der Befehl binomCDF(n, p, k) berechnet automatisch:
\( P(X \le {\textcolor{blue}{k}}) \)
Das heißt: alle Trefferzahlen von 0 bis k werden berücksichtigt.

So sieht das am Taschenrechner konkret aus:

Wir geben die Werte aus unserem Beispiel ein:
binomCDF(10, 1/6, 3), also:
\(n = 10\)
\( p= 1/6 \)
\(k = 3\)
Der Taschenrechner addiert alle Einzelwahrscheinlichkeiten von
\( X = 0 \) bis \( X = {\textcolor{blue}{3}} \).
\( P(X \le {\textcolor{blue}{3}}) \approx \textcolor{midnightblue}{0{,}9302} \)

Arbeiten mit dem Taschenrechner

Ein kleines Problem beim Taschenrechner: binomCDF kann nur höchstens rechnen, also \( P(X \le k) \).

Du wirfst \( {\textcolor{orange}{10}} \)-mal einen Würfel.
Treffer: jede gewürfelte 5.
Wie wahrscheinlich ist es, mindestens \( {\textcolor{blue}{6}} \) Treffer zu erzielen?

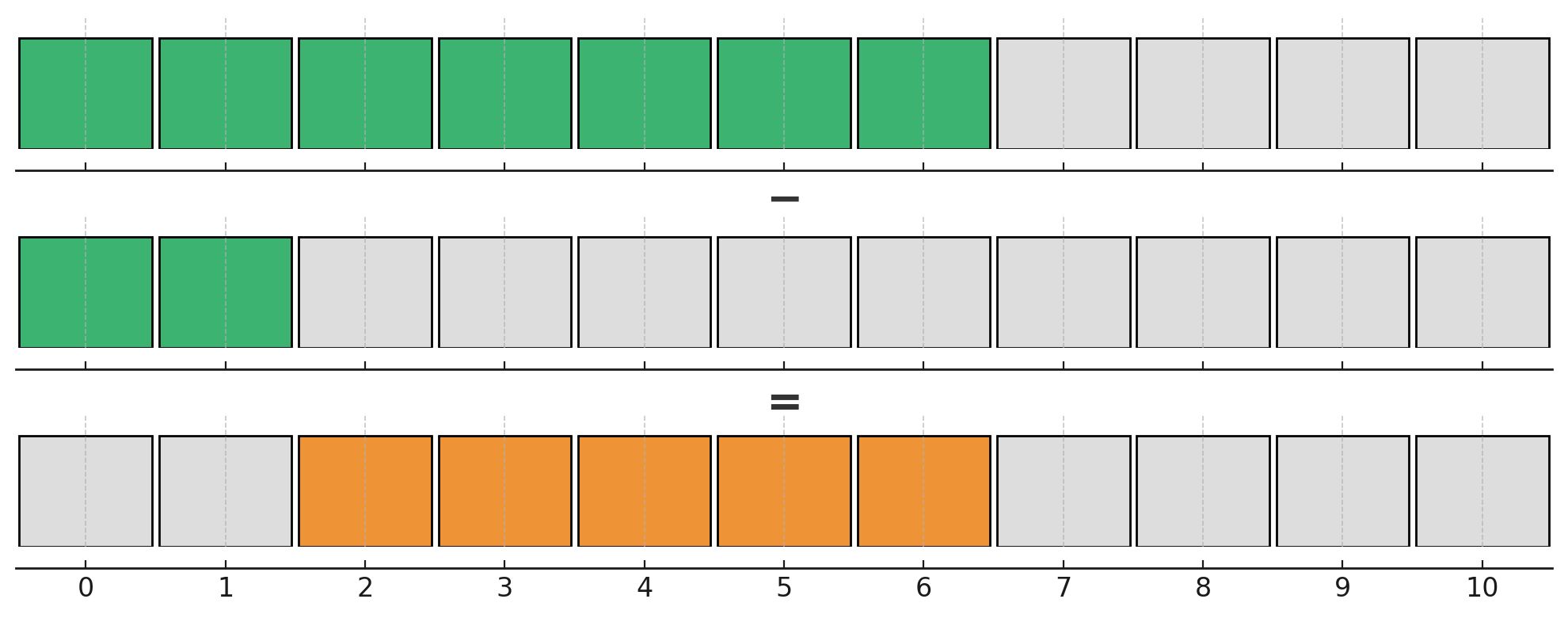
Wir schauen uns das am Zahlenstrahl an:

Orange: das wollen wir berechnen.
Grün: das kann der Taschenrechner rechnen.

Um mit dem Taschenrechner arbeiten zu können, müssen wir zunächst den grünen Bereich berechnen.

Aus \( {\textcolor{orange}{P(X \ge 6)}} \)
wird \( {\textcolor{green}{P(X \le 5)}} \)

Jetzt rechnen wir mit dem Taschenrechner:

\( {\textcolor{green}{\text{binomCDF}(10, \dfrac{1}{6}, 5)}} = {\textcolor{green}{0{,}9976}} \)

Das ist der grüne Bereich. Gesucht ist der orangene Bereich.

Beide sind Gegenteile → wir nutzen das Gegenereignis.

\( {\textcolor{orange}{P(X \ge 6)}} = 1 - {\textcolor{green}{P(X \le 5)}} \)
\( = 1 - {\textcolor{green}{0{,}9976}} \)
\( = {\textcolor{orange}{0{,}0024}} \)
→ Die Wahrscheinlichkeit, mindestens 6 Treffer zu erzielen, beträgt etwa 0,24 %.
Merke
Der TR kann nur höchstens rechnen: \( P(X \le k) \)
Typische Umformungen:
\( {\textcolor{orange}{P(X \ge k)}} = 1 - {\textcolor{green}{P(X \le k-1)}} \)
\( {\textcolor{orange}{P(X > k)}} = 1 - {\textcolor{green}{P(X \le k)}} \)
\( {\textcolor{orange}{P(X < k)}} = {\textcolor{green}{P(X \le k-1)}} \)
\( {\textcolor{orange}{P(a \le X \le b)}} = {\textcolor{green}{P(X \le b)}} - {\textcolor{green}{P(X \le a-1)}} \)

Wie du siehst gibt es noch weitere Situationen, in denen du für den Taschenrechner umformen musst – immer dann, wenn dort nicht direkt \( P(X \le k) \) steht.

Gesucht: \( {\textcolor{orange}{P(X > 2)}} \)

Orange: das wollen wir berechnen.
Grün: das kann der Taschenrechner rechnen.

\( {\textcolor{orange}{P(X > 2)}} = 1 - {\textcolor{green}{P(X \le 2)}} \)
Gesucht: \( {\textcolor{orange}{P(X < 5)}} \)
\( {\textcolor{orange}{P(X < 5)}} = {\textcolor{green}{P(X \le 4)}} \)

Der gesuchte Bereich liegt bereits auf derselben Seite wie der TR-Bereich – ein Gegenereignis brauchst du hier nicht, wir passen nur die Grenzen an.

Gesucht: \( {\textcolor{orange}{P(2 \le X \le 6)}} \)

Wir schauen zuerst auf den Zahlenstrahl:

Der Taschenrechner kann nur links rechnen: \( {\textcolor{green}{P(X \le k)}} \).

Also bauen wir den Bereich 2 bis 6 aus zwei TR-Bereichen:

\( {\textcolor{orange}{P(2 \le X \le 6)}} = {\textcolor{green}{P(X \le 6)}} - {\textcolor{green}{P(X \le 1)}} \)

Zuerst der Bereich bis zur 6:

\( {\textcolor{green}{P(X \le 6)}} = {\textcolor{green}{0{,}9996}} \)

Dann der Bereich bis zur 2 (ist zu viel, muss weg):

\( {\textcolor{green}{P(X \le 1)}} = {\textcolor{green}{0{,}4843}} \)

Jetzt bleibt genau der mittlere Bereich übrig:

\( {\textcolor{orange}{P(2 \le X \le 6)}} = {\textcolor{green}{0{,}9996}} - {\textcolor{green}{0{,}4843}} \)
\( = {\textcolor{orange}{0{,}5153}} \)
→ Zwischen 2 und 6 Treffern liegt die Wahrscheinlichkeit bei 51,53 %.
Die Binomialverteilung fasst viele einzelne Zufallsexperimente zusammen. Wie ein einzelnes Bernoulli-Experiment berechnet wird, zeigen wir dir in der Bernoulli-Formel.

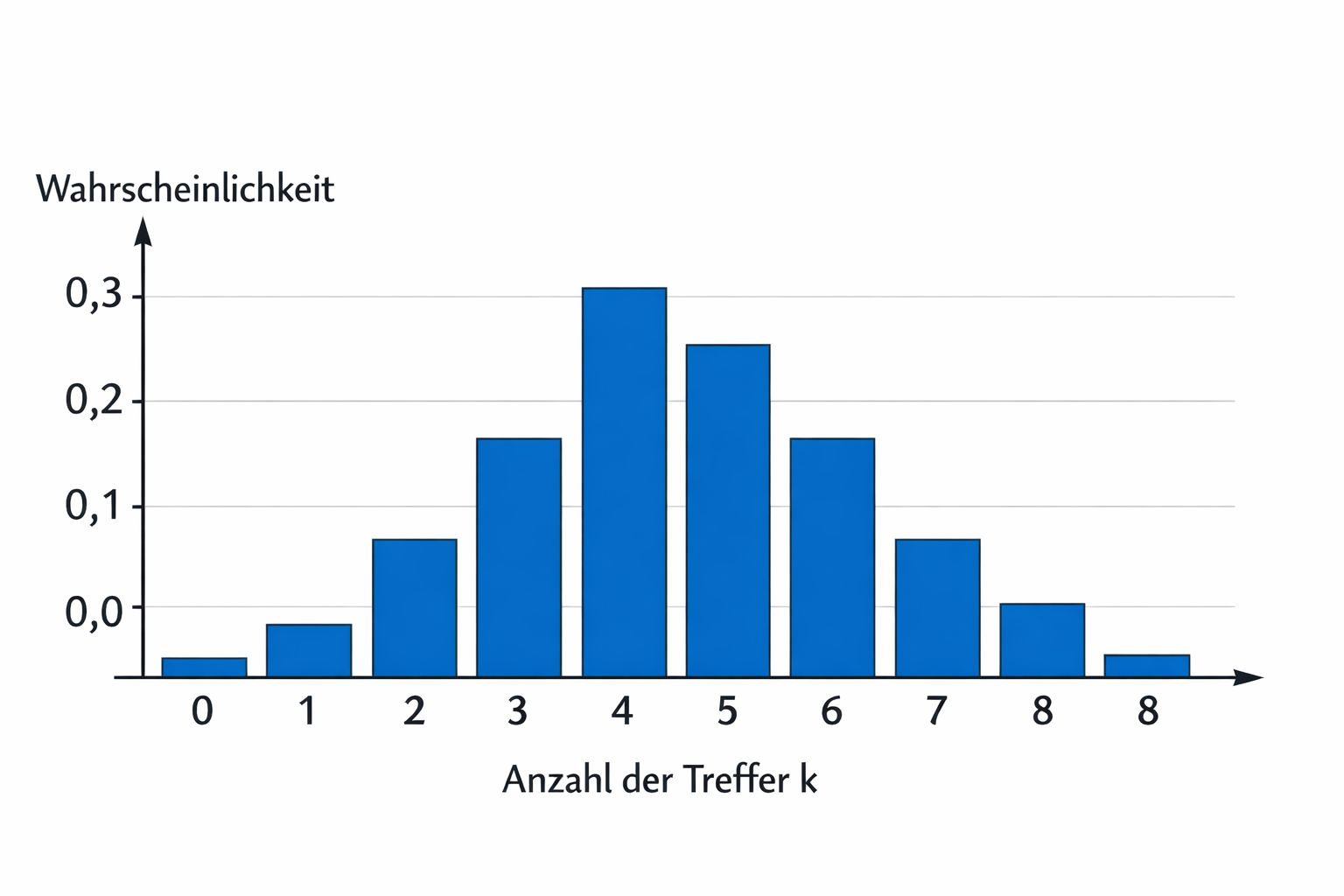
Histogramme erstellen

Ein Histogramm macht die Binomialverteilung sichtbar: Jede Trefferzahl \(k\) bekommt einen Balken – und die Balkenhöhe ist die Wahrscheinlichkeit \(P(X=k)\).

\(X\) ist binomialverteilt mit: \( \textcolor{orange}{n = 6} \quad \textcolor{green}{p = 0{,}15} \)
Wir brauchen die Wahrscheinlichkeiten \(P(X=k)\) für jede Trefferanzahl \( \textcolor{blue}{k} \).
Taschenrechner
Für einzelne Balken nutzt du: binomPDF(n, p, k)
\( P(X = \textcolor{blue}{k}) \)
→ Das liefert dir die Wahrscheinlichkeit und damit die Höhe des Balkens im Histogramm.
\( P(X=\textcolor{blue}{0}) \approx 0{,}3771 \)
\( P(X=\textcolor{blue}{1}) \approx 0{,}3993 \)
\( P(X=\textcolor{blue}{2}) \approx 0{,}1762 \)
\( P(X=\textcolor{blue}{3}) \approx 0{,}0415 \)
\( P(X=\textcolor{blue}{4}) \approx 0{,}0055 \)
\( P(X=\textcolor{blue}{5}) \approx 0{,}0004 \)
\( P(X=\textcolor{blue}{6}) \approx 0{,}0000 \)

Ein Histogramm hat auf der x-Achse alle Werte für \(k\) und auf der y-Achse die Wahrscheinlichkeit.

Über jedem \(k\) zeichnest du einen Balken – so hoch wie \(P(X=k)\), die berechnete Wahrscheinlichkeit.

Im Histogramm siehst du die Verteilung der Wahrscheinlichkeiten – am höchsten Balken kannst du den Erwartungswert abschätzen.

Histogramme zeigen nicht nur Wahrscheinlichkeiten, sondern auch, wo die Werte typischerweise liegen und wie stark sie streuen. Was genau Erwartungswert und Standardabweichung bedeuten, erklären wir dir im Beitrag Erwartungswert und Standardabweichung .
Merke
Ein Histogramm zeigt Wahrscheinlichkeiten, keine Häufigkeiten.
• x-Achse: mögliche Trefferzahlen \(k\)
• Balkenhöhe: Wahrscheinlichkeit \( P(X = k) \)
→ Je höher der Balken, desto wahrscheinlicher ist dieses Ergebnis.

Du suchst Profi-Nachhilfe mit echtem Impact? Dann bist du bei OnMathe genau richtig!

Verstehe Mathe ab der ersten Stunde.

Profi-Nachhilfe in Mathe
Student lernt draußen im freien mit Notebook

Teste dein Wissen

Übungen

Ein Quiz besteht aus \( {\textcolor{orange}{7}} \) Fragen.
Die Wahrscheinlichkeit, eine Frage richtig zu beantworten, beträgt \( {\textcolor{green}{0{,}3}} \).
Wie groß ist die Wahrscheinlichkeit für genau \( {\textcolor{blue}{2}} \) richtige Antworten?

Lösung

Gesucht: \( P(X = {\textcolor{blue}{2}}) \)
\( \text{binomPDF}(7,0{,}3,2) \approx 0{,}317 \)

Ein Basketballspieler wirft \( {\textcolor{orange}{8}} \)-mal auf den Korb.
Die Trefferwahrscheinlichkeit beträgt \( {\textcolor{green}{0{,}4}} \).
Wie groß ist die Wahrscheinlichkeit für höchstens \( {\textcolor{blue}{2}} \) Treffer?

Lösung

\( P(X \le {\textcolor{blue}{2}}) \)
\( \text{binomCDF}(8,0{,}4,2) \approx 0{,}315 \)

Ein Glücksrad wird \( {\textcolor{orange}{12}} \)-mal gedreht.
Die Trefferwahrscheinlichkeit beträgt \( {\textcolor{green}{0{,}25}} \).
Wie wahrscheinlich sind mindestens \( {\textcolor{blue}{4}} \) Treffer?

Lösung

\( P(X \ge {\textcolor{blue}{4}}) = 1 - P(X \le 3) \)
\( = 1 - \text{binomCDF}(12,0{,}25,3) \approx 0{,}647 \)

Ausgewählt für Dich

Empfohlene Beiträge

Bernoulli-Ketten erkennen, Formel einsetzen, Wahrscheinlichkeiten berechnen – ganz ohne Panik.

Die Bernoulli-Formel: Grundlagen der Binomialverteilung

Bernoulli-Ketten erkennen, Formel einsetzen, Wahrscheinlichkeiten berechnen – ganz ohne Panik.

Was sagen Erwartungswert und Standardabweichung? So findest du heraus, was bei Zufallsversuchen am wahrscheinlichsten ist.

Binomialverteilung: Erwartungswert & Standardabweichung

Was sagen Erwartungswert und Standardabweichung? So findest du heraus, was bei Zufallsversuchen am wahrscheinlichsten ist.

Mehr dazu

in unseren FAQs

Wann kann ich den Taschenrechner direkt mit binomCDF benutzen?

Immer dann, wenn in der Aufgabe \( P(X \le k) \) gesucht ist.
→ Der Taschenrechner rechnet von 0 bis k.

Was mache ich bei „mindestens“ oder „größer als“?

Dann musst du die Aufgabe umformen.
→ Du berechnest zuerst den passenden TR-Bereich und nutzt das Gegenereignis.

Wann brauche ich kein Gegenereignis?

Wenn der gesuchte Bereich bereits links liegt, zum Beispiel bei \( P(X < k) \).
→ Dann passt du nur die Grenze an: \( P(X \le k-1) \).

Wofür ist binomPDF gut?

Mit binomPDF berechnest du Einzelwahrscheinlichkeiten.
→ Genau diese Werte sind die Balkenhöhen im Histogramm.

Was zeigt ein Histogramm bei der Binomialverteilung?

Es zeigt, wie sich die Wahrscheinlichkeiten auf die Trefferzahlen verteilen.
→ Hohe Balken bedeuten: dieses Ergebnis ist wahrscheinlicher.

Mehr dazu

Weiterführende Informationen

Kumulierte Wahrscheinlichkeiten im Histogramm

Ein Histogramm ist die grafische Darstellung einer Binomialverteilung. Es zeigt dir also die Wahrscheinlichkeiten für alle möglichen Trefferzahlen in einer Bernoulli-Kette.

Ein Basketballspieler trifft einen Freiwurf mit der Wahrscheinlichkeit \( {\textcolor{green}{p = \tfrac{1}{6}}} \).
Er wirft insgesamt \( {\textcolor{orange}{10}} \)-mal.
Wie wahrscheinlich ist es, höchstens \( {\textcolor{blue}{3}} \) Treffer zu erzielen?

„Höchstens 3 Treffer“ bedeutet: Wir zählen alle Fälle mit

\( {\textcolor{blue}{k}} = {\textcolor{orange}{0}},\;{\textcolor{orange}{1}},\;{\textcolor{orange}{2}},\;{\textcolor{orange}{3}} \)

Im Histogramm sind das genau die orangenen Balken (von links).

Wichtig
Bei „höchstens \(k\) Treffern“ musst du immer bei 0 starten.
0, 1, 2, …, \(k\)
Die 0 Treffer gehören also immer dazu und dürfen nicht vergessen werden.
Merke
  • Ein Balken steht für eine Trefferzahl \( {\textcolor{blue}{k}} \).
  • „Höchstens \( {\textcolor{blue}{3}} \) Treffer“ bedeutet: alle Balken von \( {\textcolor{blue}{0}} \) bis \( {\textcolor{blue}{3}} \).
  • Die kumulierte Wahrscheinlichkeit ist dann:
    Summe dieser Balken \( \Rightarrow P(X \le {\textcolor{blue}{3}}) \)

Genau diese Summe mehrerer Balken ist eine kumulierte Wahrscheinlichkeit.

PDF oder CDF - den Taschenrechner richtig nutzen

Beim Taschenrechner gibt es bei der Binomialverteilung zwei wichtige Befehle: binomPDF und binomCDF.

Der Unterschied liegt darin, wie viele Wahrscheinlichkeiten der Taschenrechner berechnet.

binomPDF
binomPDF(n, p, k)
\( P(X = \textcolor{blue}{k}) \)
Der Taschenrechner berechnet hier die Wahrscheinlichkeit für genau eine Trefferzahl \(k\).
→ Es wird nur ein einzelner Wert berechnet.
→ Im Histogramm entspricht das genau einem Balken.
binomCDF
binomCDF(n, p, k)
\( P(X \le \textcolor{blue}{k}) \)
Der Taschenrechner berechnet hier alle Wahrscheinlichkeiten von \(X = 0\) bis \(X = k\).
Diese einzelnen Wahrscheinlichkeiten werden addiert.
→ Das Ergebnis ist eine kumulierte Wahrscheinlichkeit.
→ Im Histogramm sind das mehrere Balken zusammen.
Merke
PDF = ein Balken → \( P(X=\textcolor{blue}{k})\)
CDF = mehrere Balken von links → \( P(X\le\textcolor{blue}{k}) \)

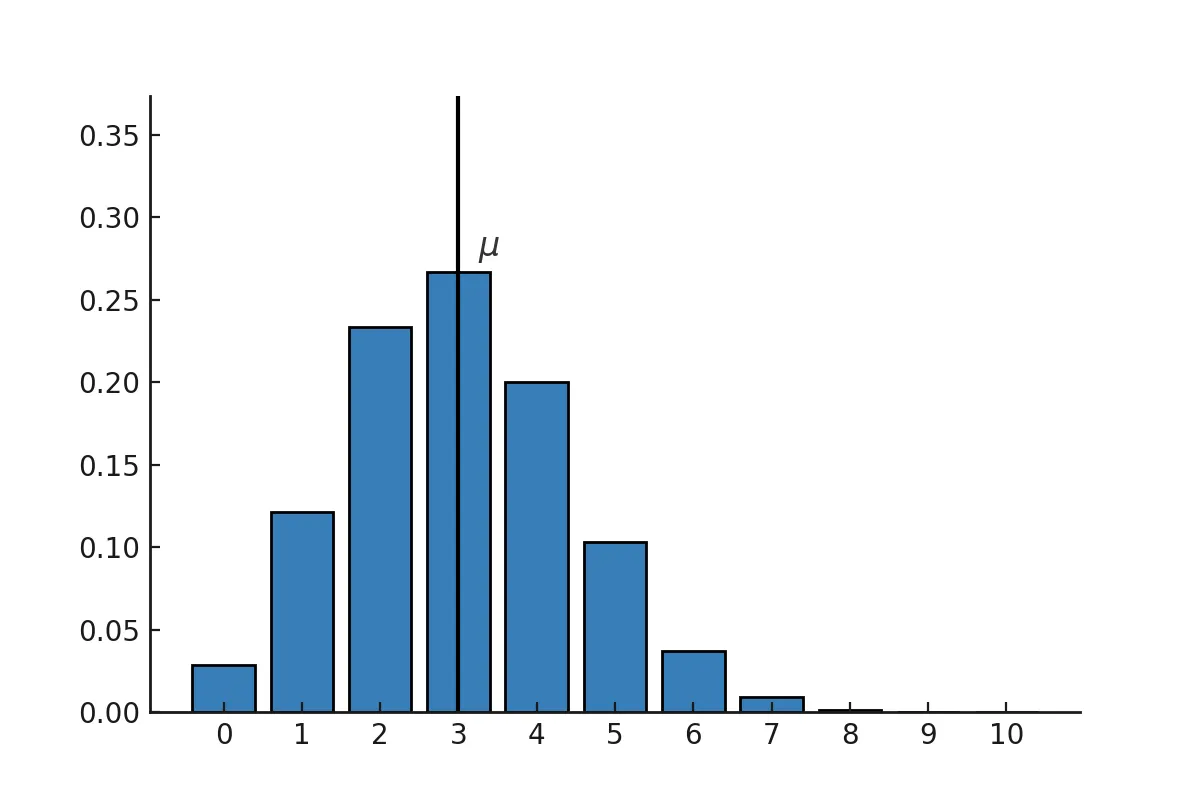
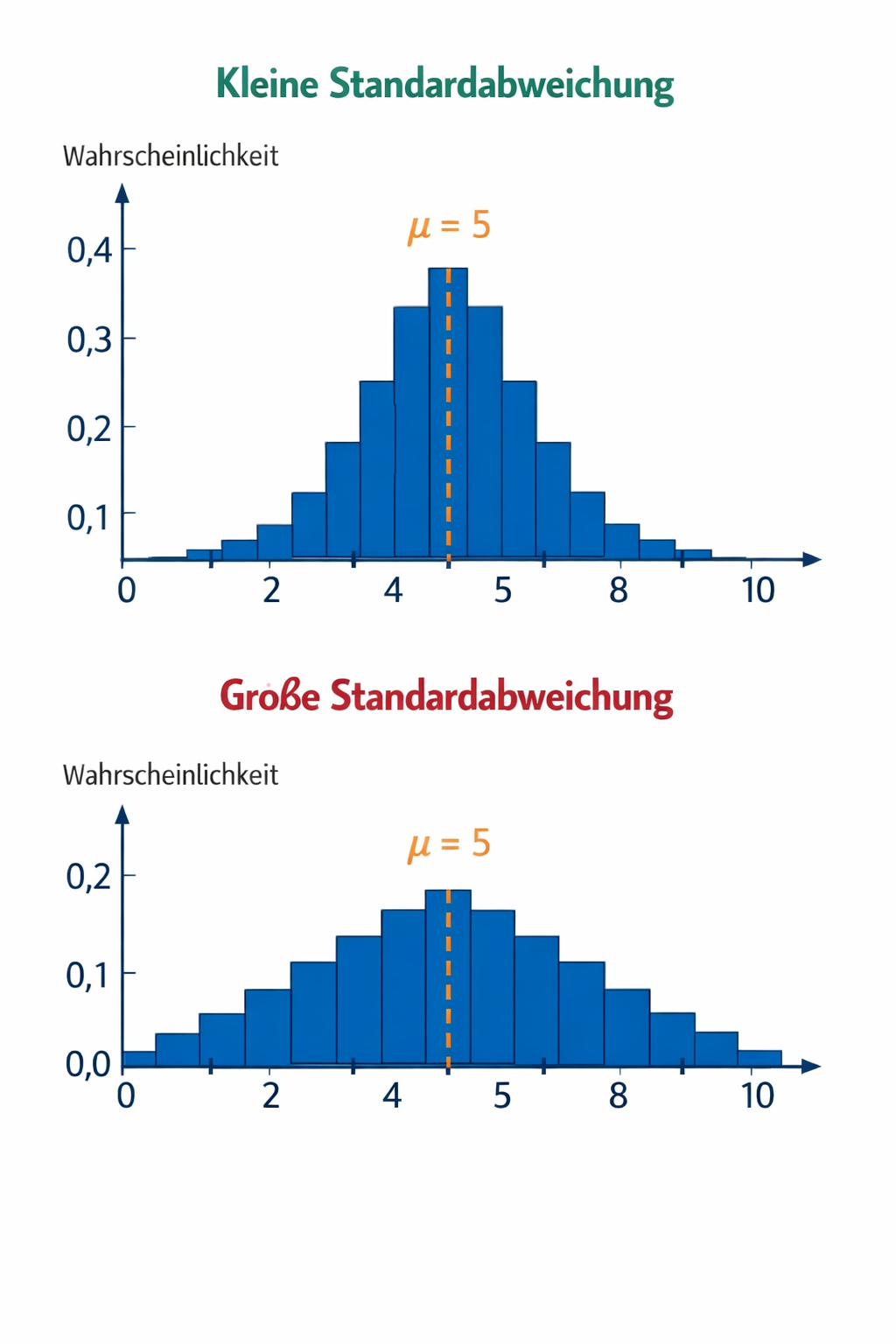
Der Erwartungswert in der Binomialverteilung

Ein Histogramm zeigt dir anschaulich, wie sich die Wahrscheinlichkeiten einer Binomialverteilung verteilen. An ihm kannst du sowohl den Erwartungswert als auch die Streuung gut erkennen.

Der Erwartungswert gibt an, wo sich die Verteilung im Durchschnitt zentriert.

\( \mu = {\textcolor{orange}{n}} \cdot {\textcolor{green}{p}} \)

Der Erwartungswert \( \mu = {\textcolor{orange}{n}} \cdot {\textcolor{green}{p}} \) liegt hier bei \( \mu = 3 \).

Im Histogramm erkennst du ihn am höchsten Balken.

→ Der höchste Balken liegt beim Erwartungswert.

Ist der Erwartungswert keine ganze Zahl, liegen die höchsten Balken oft links und rechts davon.

Wichtig
Ist der Erwartungswert nicht ganzzahlig, kann der höchste Balken neben dem Erwartungswert liegen.

Die Standardabweichung beschreibt, wie stark die Werte um den Erwartungswert streuen.

\( \sigma = \sqrt{{\textcolor{orange}{n}} \cdot {\textcolor{green}{p}} \cdot (1-{\textcolor{green}{p}})} \)

Im Histogramm erkennst du die Streuung daran, wie breit oder schmal die Verteilung ist.

→ Kleine Standardabweichung: schmale, hohe Verteilung
→ Große Standardabweichung: breite, flache Verteilung
Merke
• Der Erwartungswert zeigt, wo der Schwerpunkt des Histogramms liegt.
• Die Standardabweichung zeigt, wie stark die Werte streuen.
→ Beides zusammen erklärt die Form des Histogramms.
Willst du Erwartungswert und Standardabweichung noch genauer verstehen? Dann schau dir unseren Beitrag Erwartungswert und Standardabweichung an.

Typische Formulierungen in Aufgaben

Schauen wir uns jetzt die wichtigsten Aufgabenformulierungen zur Binomialverteilung an, die du in Klassenarbeiten sicher erkennen musst.

„genau 3 Treffer“

Hier ist eine ganz bestimmte Trefferzahl gemeint. Es wird nichts zusammengefasst.

→ Du berechnest genau eine Wahrscheinlichkeit.

Im Histogramm entspricht das einem einzelnen Balken.

\( P(X = {\textcolor{blue}{3}}) \)
„höchstens 3 Treffer“

Hier werden mehrere Trefferzahlen zusammengefasst.

Gezählt wird von \( {\textcolor{blue}{0}} \) bis \( {\textcolor{blue}{3}} \).

Im Histogramm sind das alle Balken links bis einschließlich 3.

\( P(X \le {\textcolor{blue}{3}}) \)
„mindestens 3 Treffer“

Hier interessieren alle Trefferzahlen ab 3 aufwärts.

Im Histogramm sind das alle Balken rechts ab 3.

Oft rechnet man hier über das Gegenereignis.

\( P(X \ge {\textcolor{blue}{3}}) \)
„mehr als 3 Treffer“

Achtung: Der Wert \( {\textcolor{blue}{3}} \) wird hier nicht mitgezählt.

\( P(X > {\textcolor{blue}{3}}) \)
„weniger als 3 Treffer“

Auch hier gilt: Der genannte Wert gehört nicht dazu.

\( P(X < {\textcolor{blue}{3}}) \)
Fazit
Jede Aufgabe lässt sich direkt in einen Ausdruck mit \( P(X \; \dots ) \) übersetzen.
→ Erst die Formulierung verstehen, dann rechnen.

Oft musst du mit zwei Bedingungen gleichzeitig arbeiten.

„mindestens 2, aber höchstens 5 Treffer“

Wir zerlegen die Formulierung zuerst in ihre beiden Teile:

•  mindestens 2 → \( X \ge 2 \)
•  höchstens 5 → \( X \le 5 \)

Beide Bedingungen gelten gleichzeitig. Zusammen ergibt sich:

\( P(2 \le X \le 5) \)

Wichtig: Es werden nicht mehrere Wahrscheinlichkeiten einzeln gerechnet, sondern ein einziges Ereignis betrachtet.

Tipp:
Lies den Ausdruck von der Mitte aus.
→ Starte bei \( X \), lies nach links und nach rechts.
„mehr als 3, aber höchstens 7 Treffer“
• mehr als 3 → \( X > 3 \)
• höchstens 7 → \( X \le 7 \)
\( P(4 \le X \le 7) \)
Wichtig
Bei kombinierten Formulierungen werden die Bedingungen zuerst sprachlich übersetzt und dann zu einem einzigen \(P(X=\dots)\) zusammengefügt.
→ Nicht getrennt rechnen, sondern einen Bereich betrachten.

Nerdecke

Die Binomialverteilung ist mehr als eine Rechenformel für Klassenarbeiten. Mathematisch beschreibt sie ein sehr spezielles, aber wichtiges Modell: die Verteilung von Trefferzahlen bei einer festen Anzahl unabhängiger Zufallsversuche.

Der entscheidende Gedanke dabei ist nicht die Rechnung, sondern die Struktur des Zufalls: Jeder einzelne Versuch hat nur zwei mögliche Ausgänge (Treffer oder kein Treffer), aber die Kombination vieler solcher Versuche erzeugt ein ganzes Spektrum an Wahrscheinlichkeiten.

Genau dieses Spektrum ist die Binomialverteilung: Sie ordnet jeder möglichen Trefferzahl eine Wahrscheinlichkeit zu und macht Zufall dadurch vorhersagbar.

Entscheidend sind dabei immer drei feste Annahmen:
• gleiche Trefferwahrscheinlichkeit bei jedem Versuch
• unabhängige Versuche
• feste Anzahl an Versuchen

Sind diese Bedingungen erfüllt, entsteht automatisch eine charakteristische Form: ein Histogramm mit einem klaren Schwerpunkt. Dieser Schwerpunkt liegt in der Nähe des Erwartungswerts und erklärt, warum manche Trefferzahlen „typischer“ sind als andere.

Warum bei der Binomialverteilung der Binomialkoeffizient auftaucht, liegt an der Anzahl möglicher Anordnungen. Das mathematische Zählprinzip dahinter erklären wir dir in der Kombinatorik.

In der Statistik und Stochastik wird die Binomialverteilung deshalb nicht isoliert betrachtet, sondern als Grundmodell, aus dem sich viele andere Verteilungen (unter bestimmten Bedingungen) annähern oder ableiten lassen.

Beispiel:
Bei großen Versuchszahlen nähert sich die Binomialverteilung oft einer Normalverteilung an.
→ Der Zufall wirkt dann „glatter“ und symmetrischer.

Für den Schulkontext ist all das nicht rechenrelevant – aber es erklärt, warum Histogramme so aussehen, wie sie aussehen, und warum Begriffe wie Erwartungswert, Streuung und kumulierte Wahrscheinlichkeit überhaupt sinnvoll sind.

Einordnung
Die Binomialverteilung ist kein Rechentrick, sondern ein Modell für strukturierten Zufall.
→ Klassenarbeiten testen das Rechnen – Mathematik erklärt das Warum.
Deine Bildung, unsere Mission – made with ☕️  in Baden-Württemberg
Kontakt
Montag - Freitag:
13:00 -18:30 Uhr
+49 7321 7589939
Jobs
BenefitsJetzt bewerben
Social
©2025. OnMathe.
Alle Rechte vorbehalten.
DatenschutzImpressum