Binomialverteilte Zufallsgrößen
Binomialverteilung: Erwartungswert & Standardabweichung
Einleitung
Den Erwartungswert verstehen
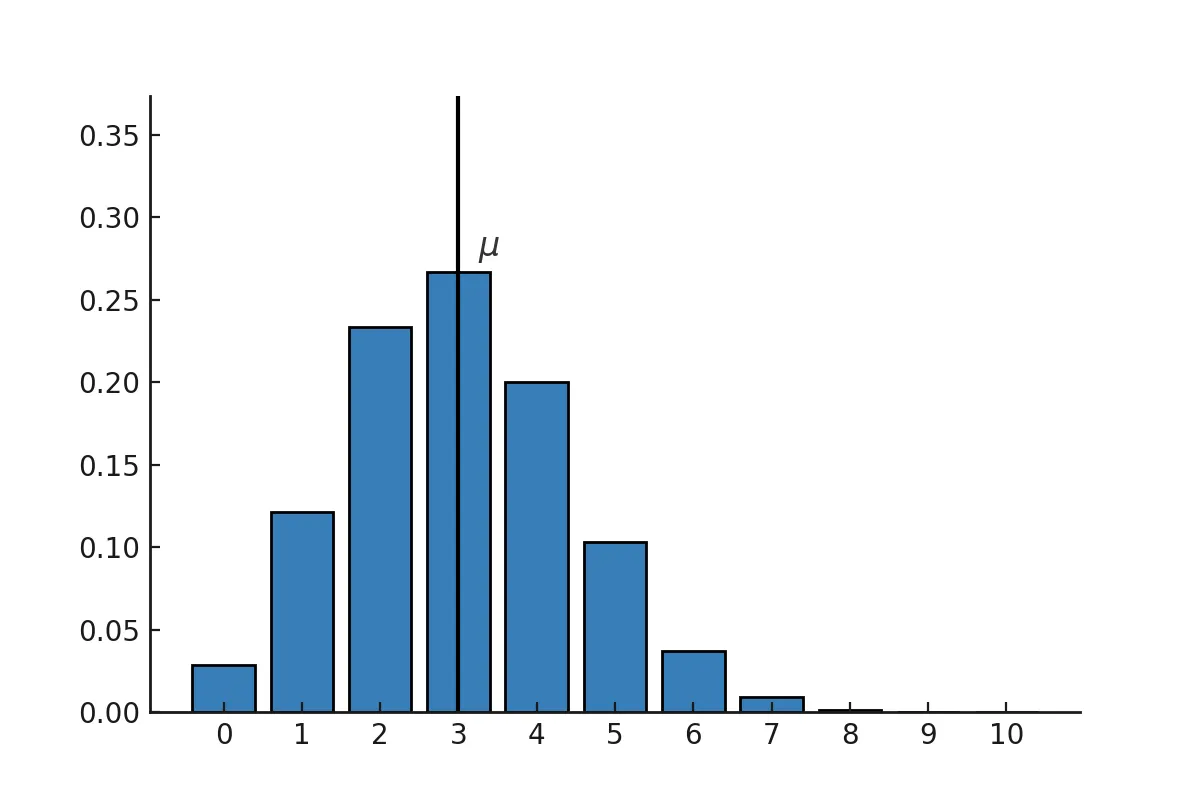
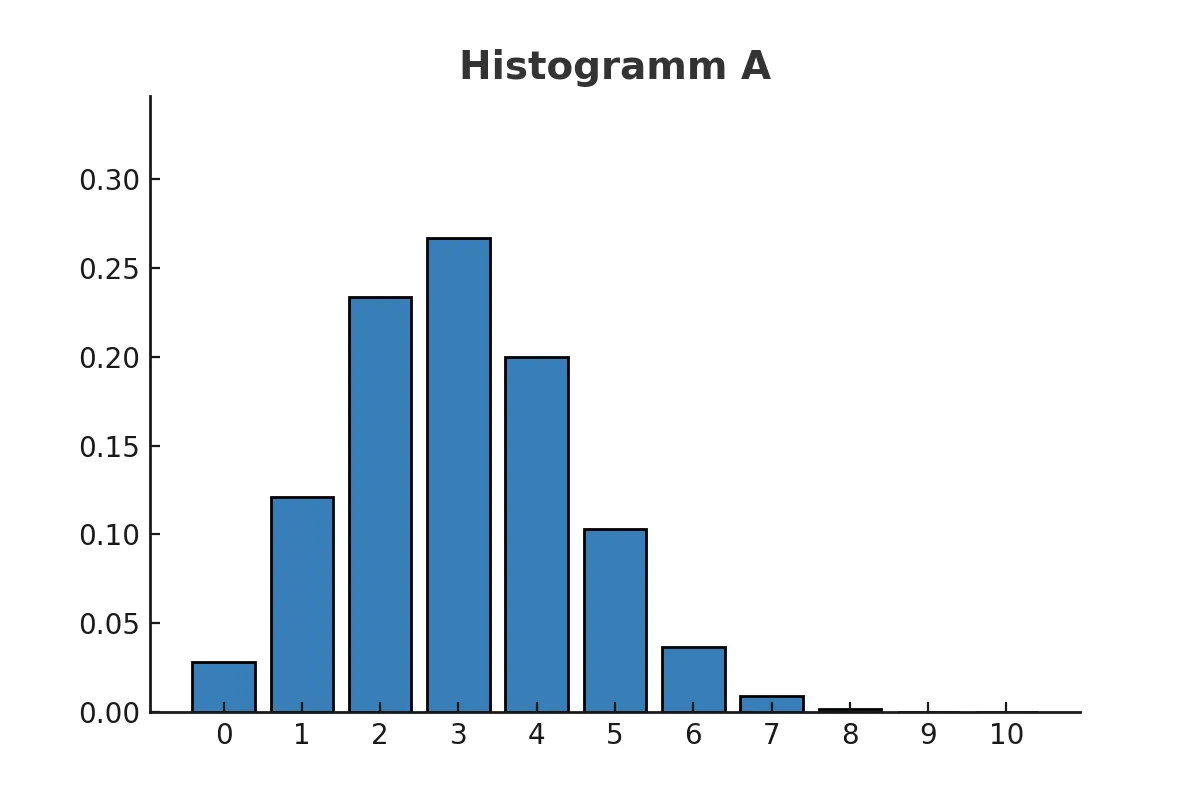
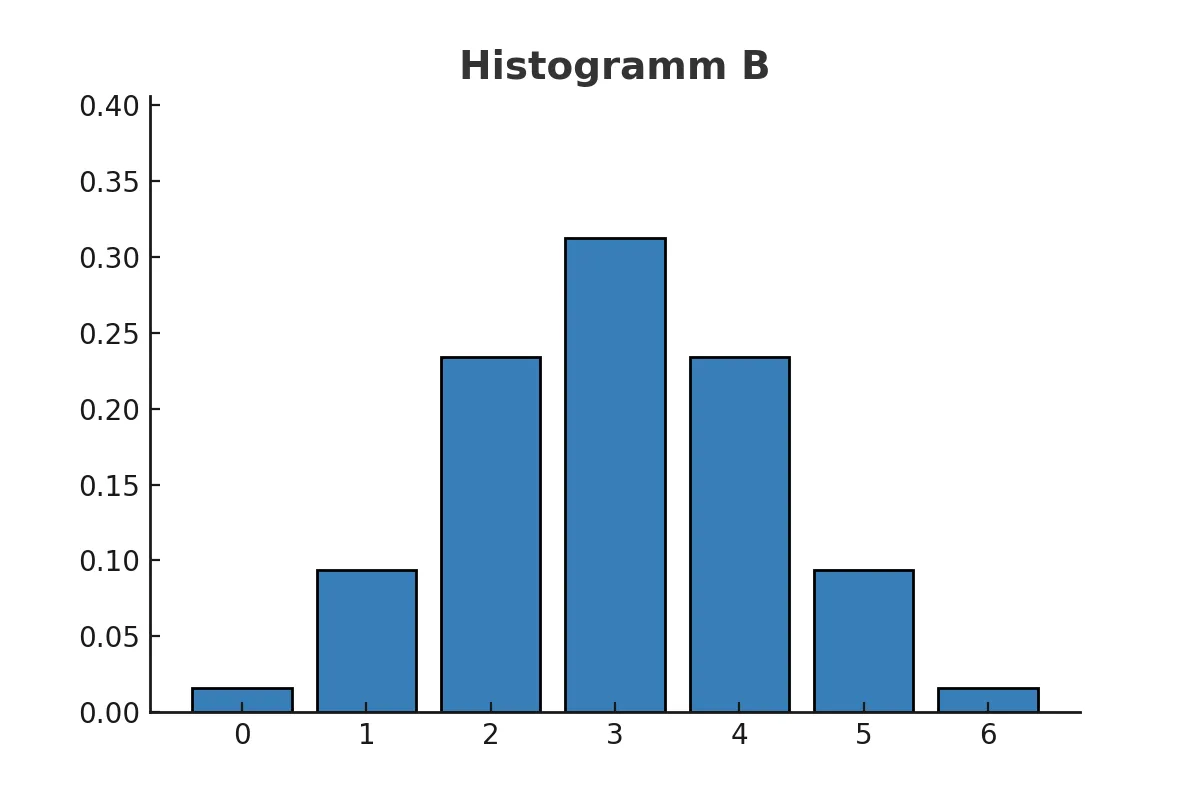
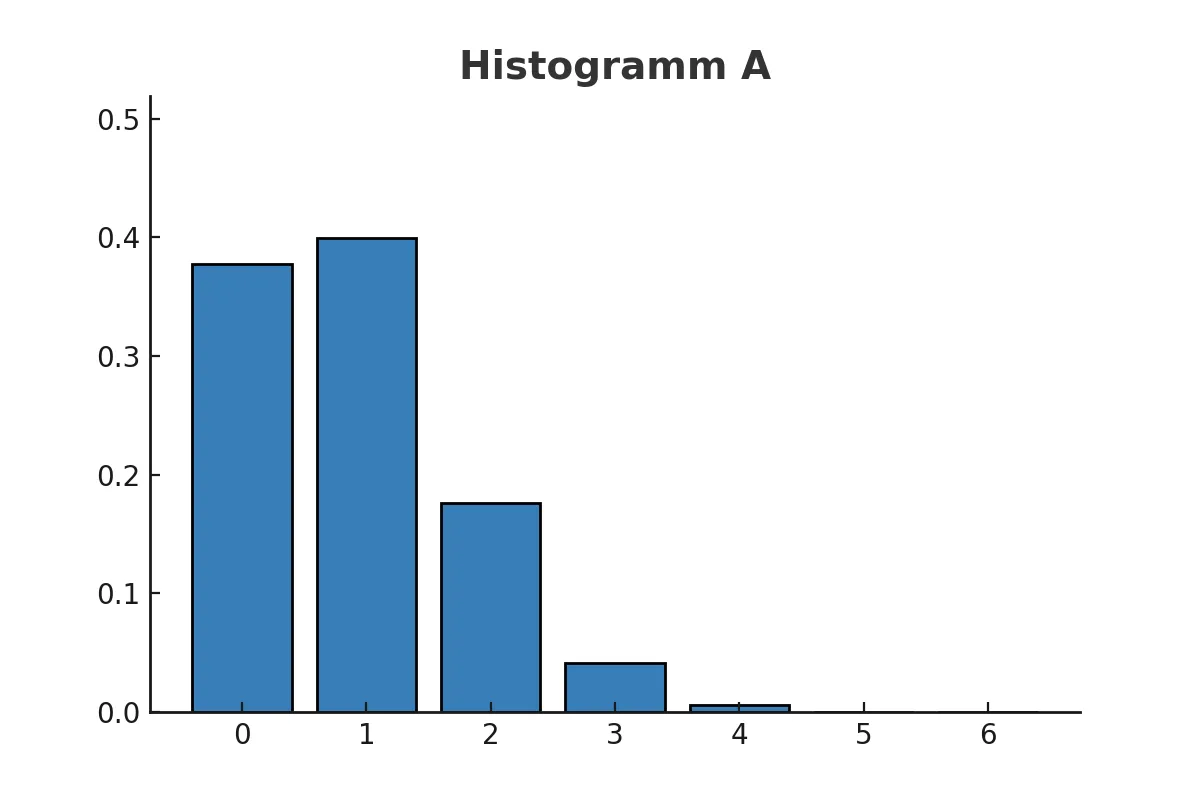
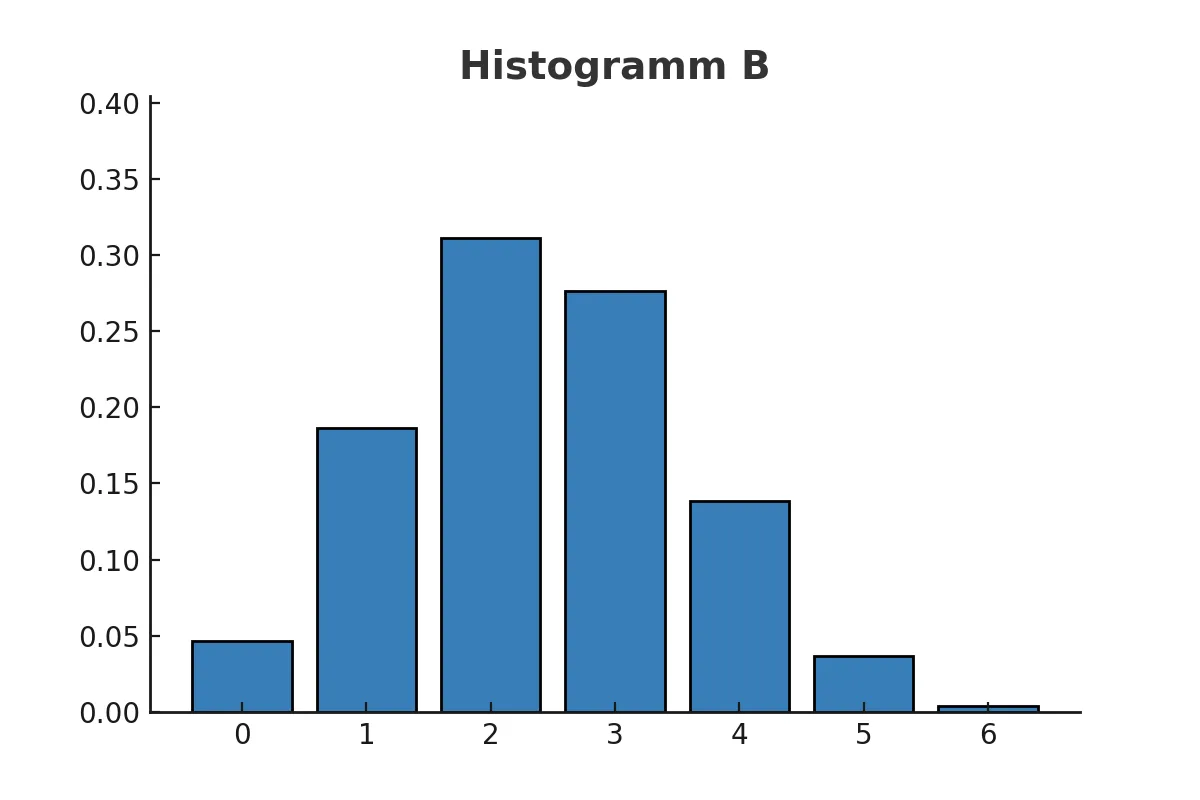
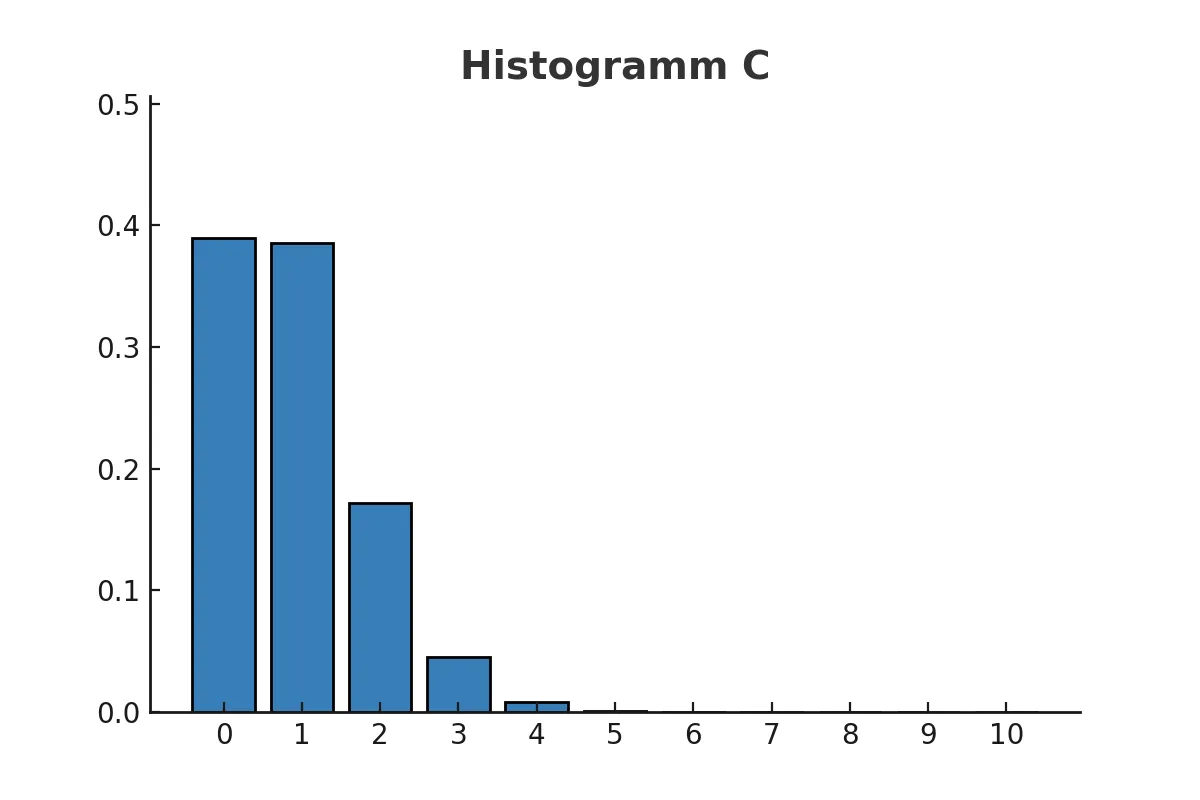
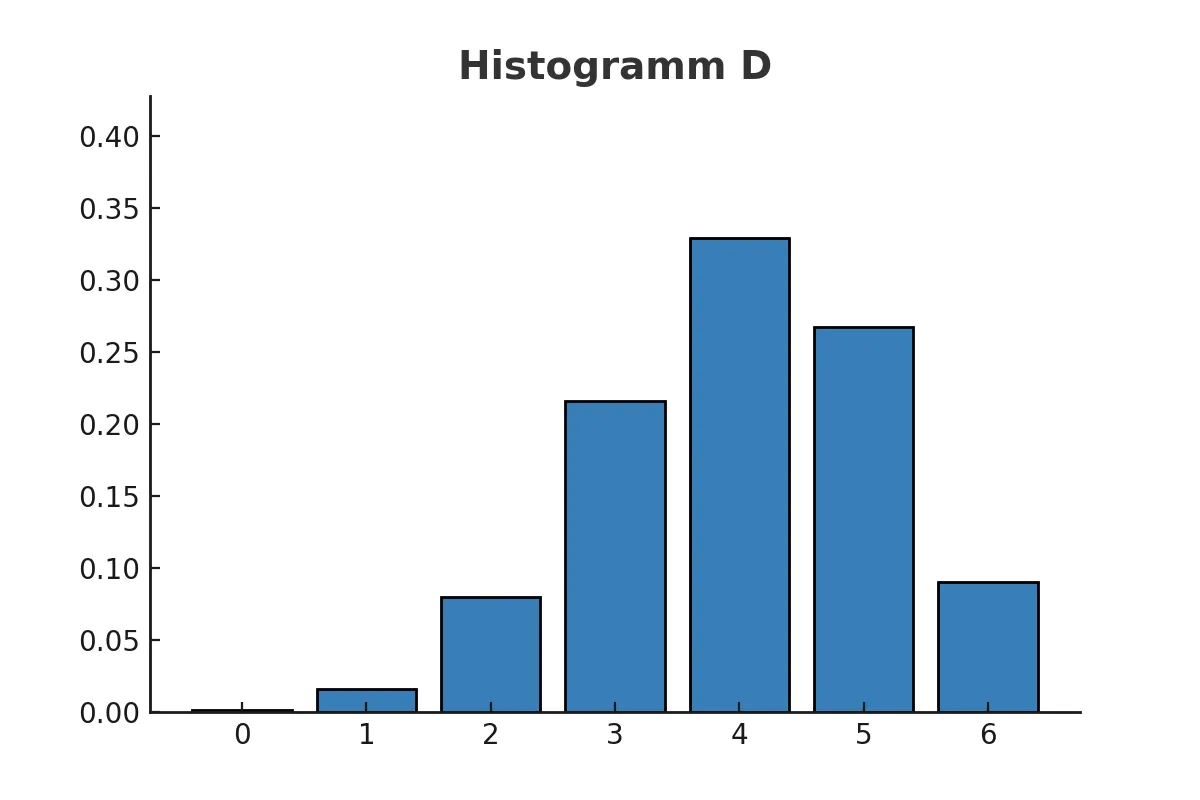
Der Erwartungswert in Histogrammen
Wenn du den Erwartungswert einer binomialverteilten Zufallsgröße kennst, ist es ganz leicht den Zufallsversuch einem Histogramm zuzuordnen. Alles was du tun musst ist im Histogramm nach dem höchsten Balken ausschau zu halten und ihn mit dem Erwartungswert zu vergleichen. Wir werden uns ein paar Beispiele dazu anschauen.
Zunächst berechnen wir den Erwartungswert der Binomialverteilung.
Mit diesem Wert können wir den Zufallsversuch einem Histogramm zuordnen.
Du siehst hier 4 verschiedene Histogramme. Um die Zuordnung zu machen, notieren wir für jedes dieser Histogramme den Wert unter dem höchsten Balken.
Die Standardabweichung
Neben dem Erwartungswert \( \mu \) gibt es auch noch die Standardabweichung \( \sigma \).
Doch, was bedeutet das nun schon wieder?
Stell dir vor: Deine ganze Klasse würfelt – jeder bekommt einen Würfel und würfelt genau 20 Mal. Was denkst du, wie oft würfelt jedes Kind eine 6?
Stimmt, dass kannst du mit dem Erwartungswert berechnen:
Das bedeutet: Die meisten Kinder werden 3 bis 4 Mal eine 6 würfeln.
Aber – natürlich längst nicht alle.
Was erwarten wir bei dem Rest? Das zeigt uns die Standardabweichung.
Die Standardabweichung sagt dir, wie stark die Ergebnisse um den Erwartungswert streuen und somit auch, was du bei der Mehrheit aller Versuche erwarten kannst, ohne dass du dich nur auf den einen Wert \( \mu \) beschränkst.
Das sieht man auch im Histogramm:
Wie du siehst liegen die höchsten Balken bei 2, 3 und 4. Der Balken bei 5 hat auch noch eine gut sichtbare Höhe, er liegt auch nur ganz knapp nicht in unserem Streuungsbereich. Der Balken bei 1 ist schon etwas niedriger, er liegt schon deutlicher neben dem Streuungsbereich. Alle Balken außerhalb des Streuungsbereiches sind nur noch sehr klein und spielen kaum noch eine Rolle.
Du siehst, auch am Histogramm kannst du erkennen, wie breit eine Wahrscheinlichkeitsverteilung streut.
Zum Vergleich schauen wir uns ein weiteres Histogramm an.
Die Standardabweichung ist mit \( \sigma = 1,94 \) größer als in unserem ersten Beispiel. Das siehst du auch daran, dass das Histogramm breiter ist. Die Höhe der Balken nimmt um den Erwartungswert deutlich langsamer ab – der Berg ist flacher und zieht sich weiter nach außen.
Zusammenfassung
Zusammenfassung & Checkliste
Du weißt jetzt, wie du bei einer binomialverteilten Zufallsgröße:
- den Erwartungswert \( \mu \) berechnest
- die Standardabweichung \( \sigma \) bestimmst
- und wie du beide Größen im Histogramm wiederfindest
Du suchst Profi-Nachhilfe mit echtem Impact? Dann bist du bei OnMathe genau richtig!
Ausgewählt für Dich
Empfohlene Beiträge
Mehr dazu
in unseren FAQs
1. Was ist der Erwartungswert?
Der Erwartungswert sagt, was im Durchschnitt bei einem Zufallsexperiment herauskommt, wenn man es sehr oft durchführt.
2. Was bedeutet die Standardabweichung?
Die Standardabweichung zeigt, wie stark die Ergebnisse vom Erwartungswert abweichen. Je kleiner sie ist, desto näher liegen die Werte am Durchschnitt.
3. Wie berechne ich den Erwartungswert bei einer Binomialverteilung?
Du multiplizierst einfach die Anzahl der Versuche (n) mit der Trefferwahrscheinlichkeit (p). Also: Erwartungswert = n · p.
4. Wann brauche ich die Standardabweichung?
Wenn du wissen willst, wie stark die Ergebnisse streuen oder wie zuverlässig der Erwartungswert ist, brauchst du die Standardabweichung.
5. Was kann ich tun, wenn der Erwartungswert keine ganze Zahl ist?
Das ist kein Problem! Der Erwartungswert muss nicht ganzzahlig sein – er ist ein Durchschnittswert und darf Kommazahlen enthalten.
Vertiefung
Weiterführende Informationen
Erwartungswert und Standardabweichung als Werkzeuge
Der Erwartungswert und die Standardabweichung helfen dir dabei, Zufallsergebnisse besser einzuschätzen. Gerade bei Zufallsversuchen mit Ja/Nein-Ausgang (z. B. Treffer oder kein Treffer) zeigen sie dir, was du im Durchschnitt erwarten kannst – und wie stark die Ergebnisse schwanken.
Was ist das?
Der Erwartungswert beschreibt den durchschnittlichen Ausgang eines Zufallsexperiments. Die Standardabweichung zeigt dir, wie weit die einzelnen Ergebnisse im Schnitt vom Durchschnitt entfernt sind. Beide Begriffe gehören zur Binomialverteilung und tauchen in vielen typischen Aufgaben auf – zum Beispiel bei Qualitätskontrollen, Tests oder Umfragen.
Mathematische Bedeutung
Die beiden Größen sind zentral für das Verständnis von Wahrscheinlichkeiten. Mit dem Erwartungswert kannst du vorhersagen, was „typisch“ ist. Die Standardabweichung hilft dir, einzuschätzen, wie stark die Ergebnisse schwanken. Gemeinsam geben sie dir ein mathematisch fundiertes Bild der Verteilung.
Häufige Fehler vermeiden
Viele verwechseln den Erwartungswert mit dem wahrscheinlichsten Wert – das ist nicht dasselbe! Auch die Standardabweichung wird oft falsch interpretiert: Sie ist kein Fehlerbereich, sondern ein Streuungsmaß. Achte außerdem darauf, dass Dezimalzahlen erlaubt sind – der Erwartungswert muss keine ganze Zahl sein.
Lerntipps
Stelle dir echte Situationen vor: Wie viele Schüler bestehen eine Prüfung? Wie viele Maschinen sind fehlerhaft? So merkst du dir den Erwartungswert leichter. Die Standardabweichung kannst du dir wie ein Maßband vorstellen: Sie zeigt, wie breit die Verteilung um den Durchschnitt ist. Rechne viele Beispiele, um ein Gefühl dafür zu bekommen.
Ursprung und Entwicklung
Der Erwartungswert ist schon seit Jahrhunderten ein wichtiges Werkzeug in der Wahrscheinlichkeitstheorie. Ursprünglich wurde er vor allem in Spielen und beim Glücksspiel verwendet. Später fand er seinen Weg in Statistik, Wirtschaft und Naturwissenschaften. Auch die Standardabweichung gehört seit dem 19. Jahrhundert zu den Grundgrößen der Wahrscheinlichkeitsrechnung.
Moderne Anwendung
Heute begegnen dir Erwartungswert und Standardabweichung überall: In der Qualitätskontrolle von Produkten, bei medizinischen Studien, in der Versicherungsbranche oder in der Datenanalyse. Sie gehören zu den Grundbegriffen, die man braucht, um statistisch denken und arbeiten zu können – und sie sind unverzichtbar für viele Prüfungen.
