Stochastik leicht gemacht

Die Bernoulli-Formel: Grundlagen der Binomialverteilung

Lisa von OnMathe
two students high five

Einleitung

Mit der Bernoulli-Formel berechnest du die Wahrscheinlichkeit für eine bestimmte Trefferanzahl \( {\textcolor{blue}{k}} \) in einer Bernoulli-Kette.
Schau dir direkt ein Beispiel an:

Aufgabe:
Ein Spieler trifft mit \( {\textcolor{green}{80\%}} \) und wirft \( {\textcolor{orange}{5}} \)-mal.
Wie wahrscheinlich sind genau \( {\textcolor{blue}{4}} \) Treffer?
Bernoulli-Formel:
\( \displaystyle P(X = {\textcolor{blue}{k}}) = \binom{{\textcolor{orange}{n}}}{{\textcolor{blue}{k}}} \cdot {\textcolor{green}{p}}^{\textcolor{blue}{k}} \cdot (1-{\textcolor{green}{p}})^{{\textcolor{orange}{n}}-{\textcolor{blue}{k}}} \)
Einzusetzende Werte:
\( {\textcolor{orange}{n = 5}}, \quad {\textcolor{green}{p = 0{,}8}}, \quad {\textcolor{blue}{k = 4}} \)
Einsetzen und ausrechnen:
\( \displaystyle P(X = {\textcolor{blue}{4}}) = \binom{{\textcolor{orange}{5}}}{{\textcolor{blue}{4}}} \cdot {\textcolor{green}{0{,}8}}^{\textcolor{blue}{4}} \cdot (1-{\textcolor{green}{0{,}8}})^{{\textcolor{orange}{5}}-{\textcolor{blue}{4}}} \)
\( P(X = {\textcolor{blue}{4}}) = 0{,}4096 \)

Im Beitrag lernst du, wie du \( {\textcolor{orange}{n}} \), \( {\textcolor{green}{p}} \) und \( {\textcolor{blue}{k}} \) aus dem Text herausliest, richtig einsetzt und typische Fehler vermeidest.

Du willst wissen, wie man mehrere Bernoulli-Experimente zusammenfasst? Dann schau dir unseren Beitrag zur Binomialverteilung an.
Merke
\( \displaystyle P(X = k) = \binom{\textcolor{orange}{n}}{\textcolor{blue}{k}} \cdot \textcolor{green}{p}^{\textcolor{blue}{k}} \cdot (1 - \textcolor{green}{p})^{\textcolor{orange}{n} - \textcolor{blue}{k}} \)
\( {\textcolor{orange}{n}} \): Anzahl der Versuche
\( {\textcolor{blue}{k}} \): Trefferanzahl (genau!)
\( {\textcolor{green}{p}} \): Trefferwahrscheinlichkeit

Inhaltsverzeichnis

Das erwartet Dich

Einleitung
Rechnen mit der Bernoulli-Formel
Die Bernoulli-Formel verstehen
Was ist ein Bernoulli-Experiment

Einleitung

Mit der Bernoulli-Formel berechnest du die Wahrscheinlichkeit für eine bestimmte Trefferanzahl \( {\textcolor{blue}{k}} \) in einer Bernoulli-Kette.
Schau dir direkt ein Beispiel an:

Aufgabe:
Ein Spieler trifft mit \( {\textcolor{green}{80\%}} \) und wirft \( {\textcolor{orange}{5}} \)-mal.
Wie wahrscheinlich sind genau \( {\textcolor{blue}{4}} \) Treffer?
Bernoulli-Formel:
\( \displaystyle P(X = {\textcolor{blue}{k}}) = \binom{{\textcolor{orange}{n}}}{{\textcolor{blue}{k}}} \cdot {\textcolor{green}{p}}^{\textcolor{blue}{k}} \cdot (1-{\textcolor{green}{p}})^{{\textcolor{orange}{n}}-{\textcolor{blue}{k}}} \)
Einzusetzende Werte:
\( {\textcolor{orange}{n = 5}}, \quad {\textcolor{green}{p = 0{,}8}}, \quad {\textcolor{blue}{k = 4}} \)
Einsetzen und ausrechnen:
\( \displaystyle P(X = {\textcolor{blue}{4}}) = \binom{{\textcolor{orange}{5}}}{{\textcolor{blue}{4}}} \cdot {\textcolor{green}{0{,}8}}^{\textcolor{blue}{4}} \cdot (1-{\textcolor{green}{0{,}8}})^{{\textcolor{orange}{5}}-{\textcolor{blue}{4}}} \)
\( P(X = {\textcolor{blue}{4}}) = 0{,}4096 \)

Im Beitrag lernst du, wie du \( {\textcolor{orange}{n}} \), \( {\textcolor{green}{p}} \) und \( {\textcolor{blue}{k}} \) aus dem Text herausliest, richtig einsetzt und typische Fehler vermeidest.

Du willst wissen, wie man mehrere Bernoulli-Experimente zusammenfasst? Dann schau dir unseren Beitrag zur Binomialverteilung an.
Merke
\( \displaystyle P(X = k) = \binom{\textcolor{orange}{n}}{\textcolor{blue}{k}} \cdot \textcolor{green}{p}^{\textcolor{blue}{k}} \cdot (1 - \textcolor{green}{p})^{\textcolor{orange}{n} - \textcolor{blue}{k}} \)
\( {\textcolor{orange}{n}} \): Anzahl der Versuche
\( {\textcolor{blue}{k}} \): Trefferanzahl (genau!)
\( {\textcolor{green}{p}} \): Trefferwahrscheinlichkeit

Rechnen mit der Bernoulli-Formel

Wir schauen uns ein weiteres Beispiel an und gehen die einzelnen Schritte bewusst langsam durch.

Eine Multiple-Choice-Frage wird mit \( {\textcolor{green}{25\%}} \) richtig beantwortet.
Es werden \( {\textcolor{orange}{6}} \) Fragen beantwortet. Wie wahrscheinlich sind genau \( {\textcolor{blue}{2}} \) richtige Antworten?

Schritt 1: Wichtige Informationen erkennen

\( {\textcolor{orange}{n}} \): Anzahl der Versuche → \( {\textcolor{orange}{n = 6}} \)
\( {\textcolor{green}{p}} \): Trefferwahrscheinlichkeit → \( {\textcolor{green}{p = 0{,}25}} \)
\( {\textcolor{blue}{k}} \): gewünschte Trefferanzahl → \( {\textcolor{blue}{k = 2}} \)
Schritt 2: Wir schreiben die Bernoulli-Formel auf und setzen ein
\( \displaystyle P(X = {\textcolor{blue}{k}}) = \binom{{\textcolor{orange}{n}}}{{\textcolor{blue}{k}}} \cdot {\textcolor{green}{p}}^{\textcolor{blue}{k}} \cdot (1-{\textcolor{green}{p}})^{{\textcolor{orange}{n}}-{\textcolor{blue}{k}}} \)
\( \displaystyle P(X = {\textcolor{blue}{2}}) = \binom{{\textcolor{orange}{6}}}{{\textcolor{blue}{2}}} \cdot {\textcolor{green}{0{,}25}}^{\textcolor{blue}{2}} \cdot (1-{\textcolor{green}{0{,}25}})^{{\textcolor{orange}{6}}-{\textcolor{blue}{2}}} \)

Schritt 3: Wir berechnen die Wahrscheinlichkeit.

\( P(X = {\textcolor{blue}{2}}) \approx 0{,}2966 \)

Die Wahrscheinlichkeit für genau zwei richtige Antworten beträgt also etwa \( 29{,}7\% \).

Wichtig
Den Ausdruck \( \displaystyle \binom{\textcolor{orange}{n}}{\textcolor{blue}{k}} \) gibst du am Taschenrechner mit der Taste nCr (oder nCk) ein.
So tippst du den Binomialkoeffizienten:
\( \displaystyle \binom{\textcolor{orange}{n}}{\textcolor{blue}{k}} \;=\; {\textcolor{orange}{n}} \ \texttt{nCr} \ {\textcolor{blue}{k}} \)
Beispiel:
\( \displaystyle \binom{\textcolor{orange}{6}}{\textcolor{blue}{2}} \;=\; {\textcolor{orange}{6}} \ \texttt{nCr} \ {\textcolor{blue}{2}} \)
Merke
\( \displaystyle P(X = k) = \binom{\textcolor{orange}{n}}{\textcolor{blue}{k}} \cdot \textcolor{green}{p}^{\textcolor{blue}{k}} \cdot (1 - \textcolor{green}{p})^{\textcolor{orange}{n} - \textcolor{blue}{k}} \)
\( {\textcolor{orange}{n}} \): Anzahl der Versuche
\( {\textcolor{blue}{k}} \): Trefferanzahl (genau!)
\( {\textcolor{green}{p}} \): Trefferwahrscheinlichkeit
In der Bernoulli-Formel steckt auch Kombinatorik. Wie der Binomialkoeffizient entsteht und was er bedeutet, erklären wir dir im Beitrag Kombinatorik.
Tipps & Tricks
  • Zuerst \( \textcolor{orange}{n}, \textcolor{blue}{k}, \textcolor{green}{p} \) aus dem Text bestimmen.
  • Binomialkoeffizient \( \displaystyle \binom{\textcolor{orange}{n}}{\textcolor{blue}{k}} \) am Taschenrechner mit nCr
  • Gegenwahrscheinlichkeit nicht vergessen: \( 1 - \textcolor{green}{p} \).
  • Dezimalwertesinnvoll runden oder als Prozentwert angeben.

Die Bernoulli-Formel verstehen

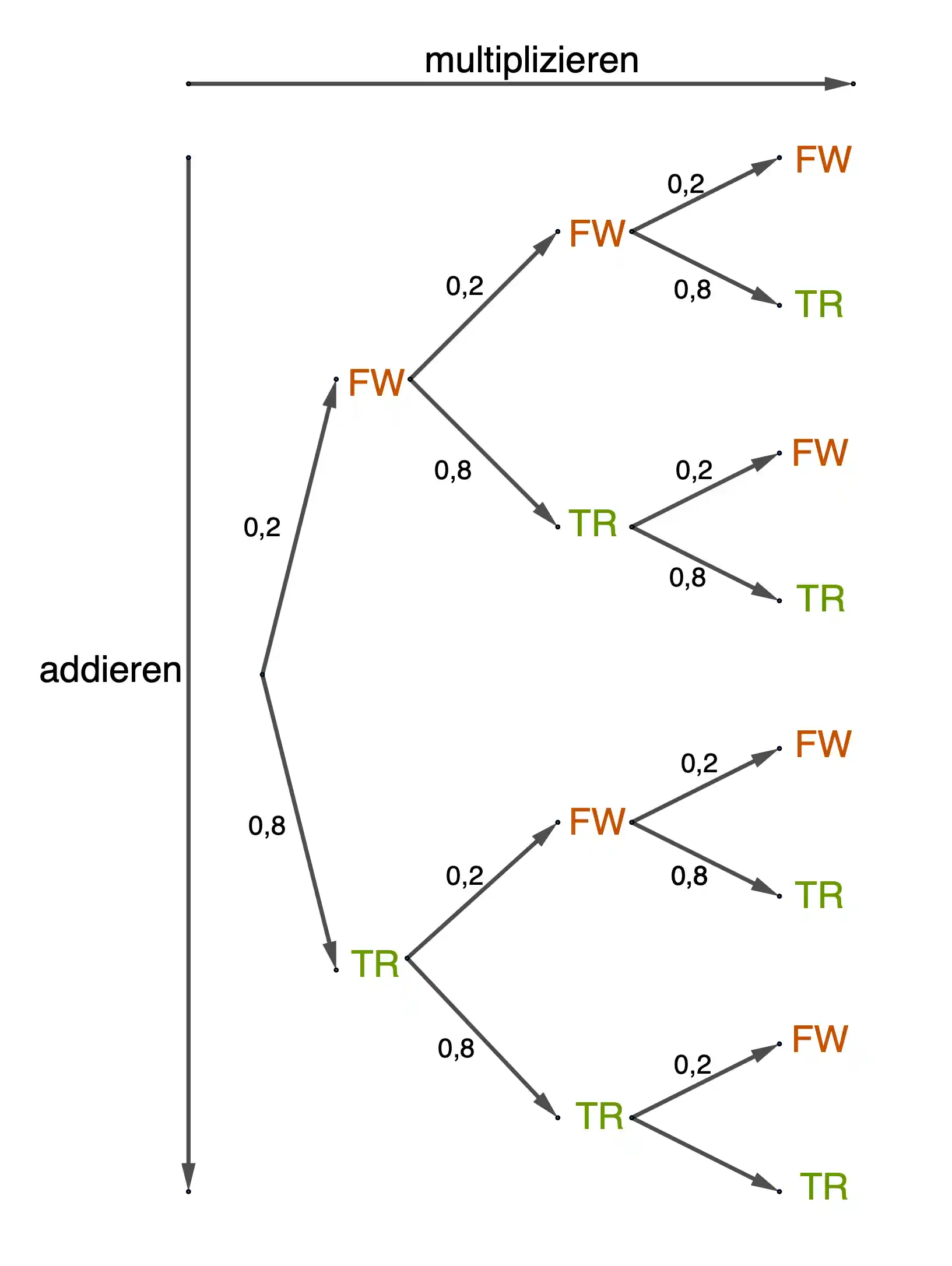
Ein Baumdiagramm zeigt dir anschaulich, wie die Bernoulli-Formel entsteht.

Trefferwahrscheinlichkeit: \( {\textcolor{green}{p = 0{,}8}} \), Würfe: \( {\textcolor{orange}{n = 3}} \)
Wie wahrscheinlich ist genau \( {\textcolor{blue}{k = 1}} \) Treffer?
Gesucht sind alle Pfade, in denen genau ein Treffer vorkommt.
→ Das sind hier insgesamt \( {\textcolor{midnightblue}{3}} \) Pfade.
Mit Pfadregeln würdest du so rechnen:
Ein Pfad:
\( {\textcolor{green}{0{,}8}} \cdot {\textcolor{orangered}{0{,}2}} \cdot {\textcolor{orangered}{0{,}2}} \)
Alle 3 Pfade:
\( 3 \cdot (0{,}8 \cdot 0{,}2 \cdot 0{,}2) \)
\( = 3 \cdot {\textcolor{green}{0{,}8}}^{\textcolor{blue}{1}} \cdot {\textcolor{orangered}{0{,}2}}^{\textcolor{blue}{2}} \)
Allgemeine Struktur:
\( = {\textsf{Anzahl Pfade}} \cdot {\textcolor{green}{\textsf{Treffer}}}^{\textcolor{blue}{\textsf{Anzahl}}} \cdot {\textcolor{orangered}{\textsf{Fehlwurf}}}^{\textcolor{blue}{\textsf{Anzahl}}} \)
Genau diese Rechnung bekommst du auch mit der Bernoulli-Formel – nur zusammengefasst.
\( \displaystyle P(X=\textcolor{blue}{k}) = \binom{\textcolor{orange}{n}}{\textcolor{blue}{k}} \cdot (\textcolor{green}{p})^{\textcolor{blue}{k}} \cdot (1-\textcolor{green}{p})^{\textcolor{orange}{n}-\textcolor{blue}{k}} \)
\( \displaystyle P(X=\textcolor{blue}{1}) \;=\; \binom{\textcolor{orange}{3}}{\textcolor{blue}{1}} \cdot (\textcolor{green}{0{,}8})^{\textcolor{blue}{1}} \cdot (1-\textcolor{green}{0{,}8})^{\textcolor{orange}{3}-\textcolor{blue}{1}} \)
\( \displaystyle =\; \binom{\textcolor{orange}{3}}{\textcolor{blue}{1}} \cdot \textcolor{green}{0{,}8}^{\textcolor{blue}{1}} \cdot \textcolor{orangered}{0{,}2}^{\textcolor{blue}{2}} \)
\( =\; \textcolor{midnightblue}{3} \cdot \textcolor{green}{0{,}8}^{\textcolor{blue}{1}} \cdot \textcolor{orangered}{0{,}2}^{\textcolor{blue}{2}} \)
\( = \textsf{Anzahl Pfade} \cdot {\textcolor{green}{\textsf{Treffer}}}^{\textcolor{blue}{\textsf{Anzahl}}} \cdot {\textcolor{orangered}{\textsf{Fehlwurf}}}^{\textcolor{blue}{\textsf{Anzahl}}} \)
→ Baumdiagramm und Bernoulli-Formel führen zum gleichen Ergebnis.
Wichtig
Beim Baumdiagramm musst du alle passenden Pfade finden und addieren.
Bei \( {\textcolor{orange}{n}} = 3 \) geht das noch. Aber bei \( {\textcolor{orange}{n}} = 20 \) wird es unmöglich.
Die Bernoulli-Formel übernimmt diese Arbeit automatisch.

Was ist ein Bernoulli-Experiment

Die Bernoulli-Formel darfst du nur anwenden, wenn du ein Bernoulli-Experiment mehrmals wiederholst und zählst, wie oft ein Treffer vorkommt.

Merke
Bedingungen für ein Bernoulli-Experiment:
  • Genau zwei Ergebnisse: Treffer / kein Treffer
  • Der Treffer ist eindeutig festgelegt
  • Die Trefferwahrscheinlichkeit ist bekannt und konstant

Schauen wir uns einige typische Beispiele an:

Du wirfst eine Münze. Treffer: Kopf.
  • Zwei Ergebnisse: Kopf oder Zahl
  • Treffer eindeutig festgelegt
  • \( \textcolor{green}{p = 0{,}5} \)
→ Bernoulli-Experiment
Du ziehst eine Kugel aus einer Urne mit 3 roten, 2 blauen und 1 grünen Kugel. Treffer: rot.
  • Treffer = rot, alle anderen = kein Treffer
  • Genau zwei Ergebnisse
  • \( \textcolor{green}{p = \dfrac{3}{6} = 0{,}5} \)
→ Bernoulli-Experiment
Du würfelst einmal und betrachtest die Augenzahl.
  • Mehr als zwei mögliche Ergebnisse
  • Kein festgelegter Treffer
→ kein Bernoulli-Experiment
Du misst die Temperatur draußen.
  • Unendlich viele mögliche Ergebnisse
  • Messung statt Treffer / kein Treffer
→ kein Bernoulli-Experiment
Wichtig
Nur zwei Ergebnisse? → mögliche Bernoulli-Situation
Messen oder mehr als zwei Ergebnisse? → keine Bernoulli-Formel
Merke
Wiederholst du ein Bernoulli-Experiment mehrmals hintereinander, entsteht eine Bernoulli-Kette.
Für eine bestimmte Trefferanzahl nutzt du dann die Bernoulli-Formel.
\( \displaystyle P(X=\textcolor{blue}{k}) = \binom{\textcolor{orange}{n}}{\textcolor{blue}{k}} \cdot \textcolor{green}{p}^{\textcolor{blue}{k}} \cdot (1-\textcolor{green}{p})^{\textcolor{orange}{n}-\textcolor{blue}{k}} \)

Du suchst Profi-Nachhilfe mit echtem Impact? Dann bist du bei OnMathe genau richtig!

Verstehe Mathe ab der ersten Stunde.

Mathe Nachhilfe online
Student lernt draußen im freien mit Notebook

Teste dein Wissen

Übungen

Gegeben: \( {\textcolor{orange}{n = 10}} \), \( {\textcolor{green}{p = 0{,}3}} \), \( {\textcolor{blue}{k = 4}} \).
Berechne \( P(X = {\textcolor{blue}{4}}) \) mit der Bernoulli-Formel.

Lösung

Bernoulli-Formel:
\( \displaystyle P(X = {\textcolor{blue}{k}}) = \binom{{\textcolor{orange}{n}}}{{\textcolor{blue}{k}}} \cdot {\textcolor{green}{p}}^{\textcolor{blue}{k}} \cdot (1-{\textcolor{green}{p}})^{{\textcolor{orange}{n}}-{\textcolor{blue}{k}}} \)
Einsetzen:
\( \displaystyle P(X = {\textcolor{blue}{4}}) = \binom{{\textcolor{orange}{10}}}{{\textcolor{blue}{4}}} \cdot {\textcolor{green}{0{,}3}}^{\textcolor{blue}{4}} \cdot (1-{\textcolor{green}{0{,}3}})^{{\textcolor{orange}{10}}-{\textcolor{blue}{4}}} \)
Ausrechnen:
\( \displaystyle P(X = {\textcolor{blue}{4}}) = 210 \cdot 0{,}3^4 \cdot 0{,}7^6 \)
\( \displaystyle P(X = {\textcolor{blue}{4}}) \approx \textcolor{midnightblue}{0{,}200} \)
→ Also etwa 20,0 %.
Tipp: \( \displaystyle \binom{10}{4} \) rechnest du mit \( {\textcolor{orange}{10}} \ \texttt{nCr} \ {\textcolor{blue}{4}} \).

Ein Spieler trifft einen Freiwurf mit \( {\textcolor{green}{p = 0{,}8}} \). Er wirft \( {\textcolor{orange}{n = 6}} \)-mal.
Wie wahrscheinlich sind genau \( {\textcolor{blue}{k = 5}} \) Treffer?

Lösung

Werte aus dem Text:
\( {\textcolor{orange}{n = 6}}, \quad {\textcolor{green}{p = 0{,}8}}, \quad {\textcolor{blue}{k = 5}} \)
Bernoulli-Formel:
\( \displaystyle P(X = {\textcolor{blue}{k}}) = \binom{{\textcolor{orange}{n}}}{{\textcolor{blue}{k}}} \cdot {\textcolor{green}{p}}^{\textcolor{blue}{k}} \cdot (1-{\textcolor{green}{p}})^{{\textcolor{orange}{n}}-{\textcolor{blue}{k}}} \)
Einsetzen:
\( \displaystyle P(X = {\textcolor{blue}{5}}) = \binom{{\textcolor{orange}{6}}}{{\textcolor{blue}{5}}} \cdot {\textcolor{green}{0{,}8}}^{\textcolor{blue}{5}} \cdot (1-{\textcolor{green}{0{,}8}})^{{\textcolor{orange}{6}}-{\textcolor{blue}{5}}} \)
Ausrechnen:
\( \displaystyle P(X = {\textcolor{blue}{5}}) = 6 \cdot 0{,}8^5 \cdot 0{,}2^1 \)
\( \displaystyle P(X = {\textcolor{blue}{5}}) \approx \textcolor{midnightblue}{0{,}393} \)
→ Also etwa 39,3 %.
Tipp: Gegenereignis: \( 1-0{,}8 = 0{,}2 \) (kein Treffer).

Ausgewählt für Dich

Empfohlene Beiträge

Binomialverteilung einfach erklärt - Mit Beispielen, Histogrammen und Tipps zur Taschenrechner-Anwendung.

Die Binomialverteilung – mit Formel & Beispielen

Binomialverteilung einfach erklärt - Mit Beispielen, Histogrammen und Tipps zur Taschenrechner-Anwendung.

Was sagen Erwartungswert und Standardabweichung? So findest du heraus, was bei Zufallsversuchen am wahrscheinlichsten ist.

Binomialverteilung: Erwartungswert & Standardabweichung

Was sagen Erwartungswert und Standardabweichung? So findest du heraus, was bei Zufallsversuchen am wahrscheinlichsten ist.

Mehr dazu

in unseren FAQs

Wann darf ich die Bernoulli-Formel verwenden?

Wenn ein Versuch mehrfach unter gleichen Bedingungen durchgeführt wird.
→ Es gibt immer nur Treffer oder kein Treffer und die Trefferwahrscheinlichkeit bleibt gleich.

Was bedeutet „genau k Treffer“?

„Genau“ heißt: nicht mehr und nicht weniger.
→ Genau \( {\textcolor{blue}{k}} \) Treffer und alle anderen Versuche sind kein Treffer.

Warum kommt in der Bernoulli-Formel auch das Gegenereignis vor?

Wenn wir Treffer zählen, müssen wir auch wissen, was in den anderen Versuchen passiert.
→ Diese Versuche sind kein Treffer und werden mit dem Gegenereignis beschrieben.

Was ist der Unterschied zwischen Bernoulli-Formel und Binomialverteilun

Die Bernoulli-Formel berechnet die Wahrscheinlichkeit für eine feste Trefferzahl.
→ Die Binomialverteilung fasst die Wahrscheinlichkeiten für alle möglichen Trefferzahlen zusammen.

Muss ich mit der Bernoulli-Formel immer per Hand rechnen

Nein.
In Klassenarbeiten wird der Taschenrechner verwendet, besonders für den Binomialkoeffizienten.
→ Wichtig ist vor allem, die Werte richtig aus dem Text zu lesen.

Mehr dazu

Weiterführende Informationen

Was ist eine Bernoulli-Kette

Eine Bernoulli-Kette entsteht, wenn man ein Bernoulli-Experiment mehrfach hintereinander ausführt.

Du wirfst eine Münze.
Treffer: Es kommt Kopf.

Dieser einzelne Münzwurf ist ein Bernoulli-Experiment:

• genau zwei Ergebnisse: Kopf oder Zahl
• Treffer ist festgelegt
• Trefferwahrscheinlichkeit immer \( {\textcolor{green}{p = 0{,}5}} \)

Jetzt werfen wir die Münze mehrmals hintereinander. So entsteht eine Bernoulli-Kette.

Auch bei vielen Würfen gilt immer:

Treffer: Kopf
Kein Treffer: Zahl
Trefferwahrscheinlichkeit bleibt: \( {\textcolor{green}{p = 0{,}5}} \)
Merke
Viele gleiche Bernoulli-Experimente hintereinander \( \Rightarrow \) Bernoulli-Kette mit:
• \( {\textcolor{orange}{n}} \): Anzahl der Wiederholungen
• \( {\textcolor{green}{p}} \): Trefferwahrscheinlichkeit
• \( {\textcolor{blue}{k}} \): Anzahl der Treffer
Für unser Beispiel gilt, wenn wir \({\textcolor{orange}{n = 10}}\) mal werfen:
\( {\textcolor{orange}{n = 10}}, \quad {\textcolor{green}{p = 0{,}5}}, \quad {\textcolor{blue}{k = 3}} \)
\( \displaystyle P(X=\textcolor{blue}{3}) = \binom{\textcolor{orange}{10}}{\textcolor{blue}{3}} \cdot \textcolor{green}{0{,}5}^{\textcolor{blue}{3}} \cdot (1-\textcolor{green}{0{,}5})^{\textcolor{orange}{10}-\textcolor{blue}{3}} \)
\( = 120 \cdot 0{,}5^3 \cdot 0{,}5^7 \)
\( \approx \textcolor{midnightblue}{0{,}117} \)
→ Die Wahrscheinlichkeit für genau 3 Treffer beträgt also etwa 11,7 %.
Würden wir diese Rechnung nun für alle möglichen Trefferzahlen (\( k = 0, 1, 2, \dots, 10 \)) durchführen und übersichtlich darstellen, entstünde eine Binomialverteilung.
Merke
  • Bernoulli-Experiment
    → ein einzelner Versuch mit genau zwei Ergebnissen
  • Bernoulli-Kette
    → viele gleiche Bernoulli-Experimente hintereinander
  • Binomialverteilung
    → Übersicht aller Wahrscheinlichkeiten für \( 0 \) bis \( {\textcolor{orange}{n}} \) Treffer

Bernoulli-Formel und Binomialverteilung

Mit der Bernoulli-Formel berechnest du immer nur die Wahrscheinlichkeit für eine feste Trefferzahl \( {\textcolor{blue}{k}} \).

Berechnen wir diese Wahrscheinlichkeit für alle möglichen Trefferzahlen, entsteht eine Binomialverteilung.

Ein Spieler trifft einen Freiwurf mit \( {\textcolor{green}{60\%}} \) Wahrscheinlichkeit.
Er wirft \( {\textcolor{orange}{8}} \)-mal.

Mögliche Trefferzahlen sind:

\( k = 0, 1, 2, \dots, 8 \)

Für jede Trefferzahl entsteht eine eigene Wahrscheinlichkeit.

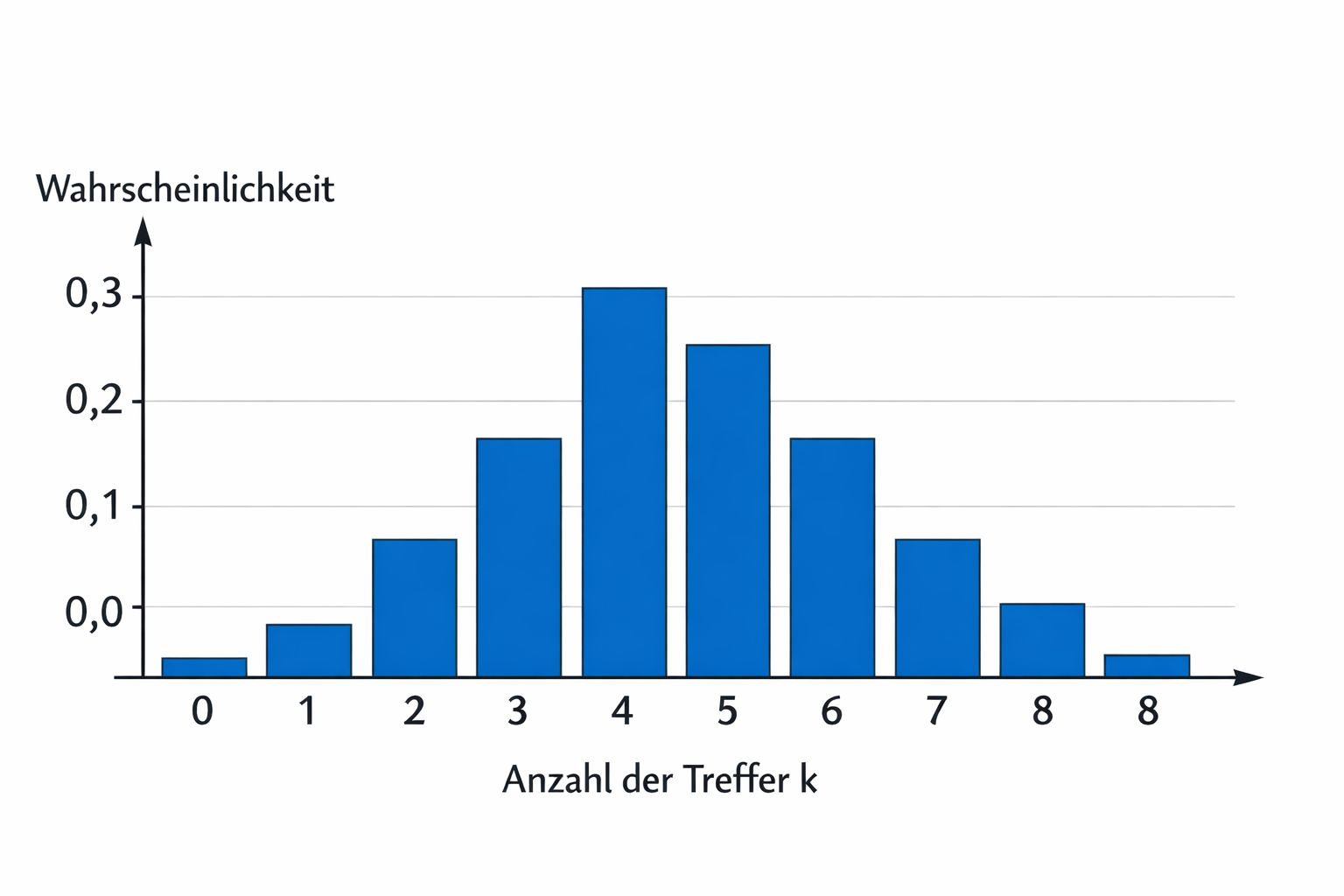
Stellt man diese einzelnen Wahrscheinlichkeiten in einem Säulendiagramm dar, entsteht ein Histogramm – die grafische Darstellung einer Binomialverteilung.

So sieht die Binomialverteilung für dieses Beispiel aus:
Jeder Balken steht für eine bestimmte Trefferzahl \( {\textcolor{blue}{k}} \).
Die Höhe des Balkens zeigt, wie wahrscheinlich diese Trefferzahl ist.
Wichtig
• ein Balken → Wahrscheinlichkeit für eine Trefferzahl \( {\textcolor{blue}{k}} \)
• alle Balken zusammen → Binomialverteilung
• Summe aller Balken → 1 (= 100 %)
• höchster Balken → am wahrscheinlichste Trefferzahl
Merke
Bernoulli-Formel
→ Wahrscheinlichkeit für genau eine Trefferzahl \( k \)
Binomialverteilung
→ Übersicht aller Wahrscheinlichkeiten für \( k = 0 \) bis \( {\textcolor{orange}{n}} \)

Aus einer Binomialverteilung lassen sich später Erwartungswert und Standardabweichung ablesen.

Das Gegenereignis in der Formel

In der Bernoulli-Formel taucht immer auch das Gegenereignis \( 1-{\textcolor{green}{p}} \) auf.

Warum das so ist, sieht man am besten an einem Beispiel.

Ein Spieler trifft einen Wurf mit \( {\textcolor{green}{p = 0{,}7}} \).
Er wirft \( {\textcolor{orange}{n = 5}} \)-mal.

Bei jedem einzelnen Wurf gibt es zwei Möglichkeiten:

Treffer: Wahrscheinlichkeit \( {\textcolor{green}{p = 0{,}7}} \)
Kein Treffer: Wahrscheinlichkeit \( 1-{\textcolor{green}{p}} = 0{,}3 \)

Suchen wir zum Beispiel die Wahrscheinlichkeit für genau \( {\textcolor{blue}{k = 2}} \) Treffer, dann gilt:

2 Treffer → 3 Fehlwürfe

Beides muss in der Rechnung vorkommen.

\( \displaystyle P(X=\textcolor{blue}{2}) = \binom{\textcolor{orange}{5}}{\textcolor{blue}{2}} \cdot ({\textcolor{green}{p}})^{\textcolor{blue}{2}} \cdot (1-{\textcolor{green}{p}})^{\textcolor{orange}{5}-\textcolor{blue}{2}} \)
Wichtig
  • Jeder Versuch endet entweder mit Treffer oder Fehlschuss.
  • Ein Fehlschuss bedeutet: kein Treffer = Gegenereignis → \( (1-{\textcolor{green}{p}}) \).
  • Die Treffer allein, sind nicht alles, auch die Fehler gehören zum Versuch.
  • In der Bernoulli-Formel steht neben \( {\textcolor{green}{p}}^{\textcolor{blue}{k}} \) für die Treffer auch \( (1-{\textcolor{green}{p}})^{\textcolor{orange}{n-k}} \) für die Anzahl der Fehlschüsse.
Merke
In der Bernoulli-Formel wird jeder Versuch vollständig erfasst:
Treffer \( \Rightarrow {\textcolor{green}{p}}^{\textcolor{blue}{k}} \) kein Treffer \( \Rightarrow (1-{\textcolor{green}{p}})^{\textcolor{orange}{n-k}} \)
Der Rest der Formel zählt nur, wie viele solcher Fälle es gibt.

Nerdecke

Warum sieht die Bernoulli-Formel genau so aus?

Die Bernoulli-Formel wirkt auf den ersten Blick wie eine reine Rechenvorschrift. Tatsächlich steckt dahinter eine sehr klare Idee.

Jede Bernoulli-Aufgabe beschreibt eine Situation mit Treffer und Fehlwurf, die sich mehrfach wiederholt.

Ein Baumdiagramm zeigt genau diese Wiederholungen: jeder Pfad steht für eine mögliche Abfolge aus Treffern und Fehlwürfen.

→ Die Bernoulli-Formel ist nichts anderes als alle passenden Pfade zusammengefasst in einer einzigen Rechnung.

Der Binomialkoeffizient \( \binom{n}{k} \) zählt dabei, wie viele dieser Pfade zu genau \( k \) Treffer führen.

Die Potenzen von \( p \) und \( 1-p \) beschreiben, wie wahrscheinlich ein einzelner Pfad mit dieser Trefferanzahl ist.

Anzahl der Pfade × Wahrscheinlichkeit eines Pfades → Gesamtwahrscheinlichkeit
Bernoulli-Formel und Binomialverteilung

Wendest du die Bernoulli-Formel nur für eine einzige Trefferzahl an, berechnest du:

\( P(X = k) \)

Berechnest du diese Wahrscheinlichkeit für alle Trefferzahlen \( k = 0, 1, 2, \dots, n \), entsteht daraus die Binomialverteilung.

Als Säulendiagramm dargestellt, siehst du sie als Histogramm.

Typischer Denkfehler
Viele Schülerinnen und Schüler verwenden die Bernoulli-Formel auch bei Aufgaben wie „höchstens“, „mindestens“ oder „zwischen“.
→ Das ist falsch.

Die Bernoulli-Formel berechnet immer nur eine ganz bestimmte Trefferzahl.

Für zusammengefasste Ereignisse musst du entweder mehrere Bernoulli-Wahrscheinlichkeiten addieren oder den Taschenrechner mit kumulierten Wahrscheinlichkeiten nutzen.

Merke
Die Bernoulli-Formel beantwortet immer nur die Frage:
Wie wahrscheinlich sind genau \( k \) Treffer?
Führt man ein Bernoulli-Experiment mehrfach hintereinander durch, entsteht die Binomialverteilung. Wie man damit rechnet und den Taschenrechner nutzt, zeigen wir dir im Beitrag zur Binomialverteilung.
Deine Bildung, unsere Mission – made with ☕️  in Baden-Württemberg
Kontakt
Montag - Freitag:
13:00 -18:30 Uhr
+49 7321 7589939
Jobs
BenefitsJetzt bewerben
Social
©2025. OnMathe. Alle Rechte vorbehalten.
DatenschutzImpressum