Stochastik leicht gemacht
Die Bernoulli-Formel: Grundlagen der Binomialverteilung
Einleitung
Rechnen mit der Bernoulli-Formel
Die Bernoulli-Formel verstehen
Um die Bernoulli-Formel zu verstehen, erinnern wir uns zuerst an das Arbeiten mit dem Baumdiagramm. Dort können wir mit den Pfadregeln Wahrscheinlichkeiten berechnen.
Im Baumdiagramm sieht das so aus:
Wir betrachten den Pfad Treffer – Fehlwurf – Fehlwurf. Um die Wahrscheinlichkeit für diesen Pfad zu berechnen, nutzen wir die Pfadregel und multiplizieren die Wahrscheinlichkeiten entlang des Pfades:
Das ist die Wahrscheinlichkeit für den Ablauf: Treffer – Fehlwurf – Fehlwurf.
Aber: Der Treffer könnte auch an einer anderen Stelle liegen. Es gibt insgesamt 3 verschiedene Pfade im Baumdiagramm, in denen genau ein Treffer steckt:
- Treffer – Fehlwurf – Fehlwurf
- Fehlwurf – Treffer – Fehlwurf
- Fehlwurf – Fehlwurf – Treffer
Alle drei Pfade haben dieselbe Wahrscheinlichkeit: \( 0{,}032 \).
Um die Gesamtwahrscheinlichkeit für genau einen Treffer zu bestimmen, müssen wir alle Einzelwahrscheinlichkeiten addieren, also alle möglichen Pfade berücksichtigen.
Damit es übersichtlicher wird, fassen wir unser Vorgehen nun Schritt für Schritt zusammen und schreiben die Berechnung der drei Pfade noch einmal ordentlich auf:
Wir haben uns noch einmal genau angeschaut, wie das Arbeiten mit dem Baumdiagramm funktioniert und haben alles übersichtlich zusammengefasst. Jetzt sehen wir, was das alles mit der Bernoulli-Formel zu tun hat.
Um den Zusammenhang zu sehen, nehmen wir noch einmal das Beispiel (Basketball, drei Würfe, genau ein Treffer), bestimmen die Werte und setzen sie in die Bernoulli-Formel ein:
- \( \textcolor{orange}{n=3} \) (Anzahl der Würfe)
- \( \textcolor{blue}{k=1} \) (genau ein Treffer)
- \( \textcolor{green}{p=0{,}8} \) (Trefferwahrscheinlichkeit pro Wurf), \( \;1-\textcolor{green}{p}=\textcolor{green}{0{,}2} \)
Wie du siehst, entspricht die Struktur der Bernoulli-Formel genau der Struktur, die wir bereits beim Arbeiten mit dem Baumdiagramm kennengelernt haben.
- Jeder Wurf hat zwei Möglichkeiten: Treffer oder Fehlschuss.
- Wenn wir nur die Treffer berücksichtigen, fehlt die Information, was in den anderen Würfen passiert.
- Deshalb brauchen wir das Gegenereignis \( (1-p) \): es beschreibt die Fehlschüsse.
- Die Exponenten \(k\) und \(n-k\) geben an, wieviele Treffer und wieviele Fehlschüsse in einem Szenario vorkommen.
Was ist ein Bernoulli-Experiment
Du suchst Profi-Nachhilfe mit echtem Impact? Dann bist du bei OnMathe genau richtig!
Ausgewählt für Dich
Empfohlene Beiträge
Mehr dazu
in unseren FAQs
1. Wann darf ich die Bernoulli-Formel verwenden?
Nur wenn es sich um eine sogenannte Bernoulli-Kette handelt – also wenn du einen Zufallsversuch mit zwei möglichen Ausgängen (Erfolg/Misserfolg) mehrmals unter denselben Bedingungen wiederholst.
2. Was ist der Unterschied zwischen einer Bernoulli-Kette und einer normalen Wahrscheinlichkeitsaufgabe?
Bei der Bernoulli-Kette bleibt die Wahrscheinlichkeit für Erfolg oder Misserfolg bei jedem Durchgang gleich – bei normalen Aufgaben kann sie sich ändern, z. B. wenn ohne Zurücklegen gezogen wird.
3. Wie erkenne ich, was in der Aufgabe „Erfolg“ ist?
Das hängt von der Fragestellung ab. Meist steht in der Aufgabe, was genau als Treffer oder Erfolg gezählt werden soll – z. B. „mindestens 3 Sechsen“, „genau 2 Treffer“ oder „höchstens ein Fehler“.
4. Muss ich die Formel auswendig lernen?
Nein, wichtiger ist, dass du sie verstehst. Wenn du weißt, wie sie aufgebaut ist und was die Bestandteile bedeuten, kannst du sie in jeder Situation richtig anwenden – auch mit Formelsammlung.
5. Was mache ich, wenn der Taschenrechner kein nCr oder keine Potenzierung kann?
Dann kannst du die Wahrscheinlichkeit auch Schritt für Schritt mit der Fakultät und der Potenzregel berechnen. Bei Klassenarbeiten wird meist ein Taschenrechner mit Kombinationsfunktion bereitgestellt.
Vertiefung
Weiterführende Informationen
Die Bernoulli-Formel als Werkzeug
Die Bernoulli-Formel ist ein zentrales Hilfsmittel in der Wahrscheinlichkeitsrechnung, wenn du mehrfache, gleichartige Versuche mit nur zwei möglichen Ausgängen untersuchst – also sogenannte Bernoulli-Ketten. Du brauchst sie immer dann, wenn du die Wahrscheinlichkeit dafür berechnen möchtest, wie oft ein bestimmtes Ergebnis innerhalb einer festen Anzahl an Versuchen eintritt. Egal ob Würfeln, Ziehen oder Raten – mit der Bernoulli-Formel hast du ein mächtiges Werkzeug in der Hand.
Was ist die Bernoulli-Formel?
Die Bernoulli-Formel beschreibt die Wahrscheinlichkeit, dass ein bestimmtes Ereignis bei einer festgelegten Anzahl an Wiederholungen exakt so oft eintritt. Dabei muss der Versuch binär sein, also nur zwei mögliche Ergebnisse haben – Erfolg oder Misserfolg. Die Formel selbst besteht aus drei Bausteinen: einer Kombinatorik-Komponente, einer Erfolgswahrscheinlichkeit und einer Gegenwahrscheinlichkeit. Du setzt sie genau dann ein, wenn du z. B. wissen willst, wie hoch die Wahrscheinlichkeit für „genau 3 Treffer bei 5 Versuchen“ ist.
Häufige Fehler & Tipps zum Lernen
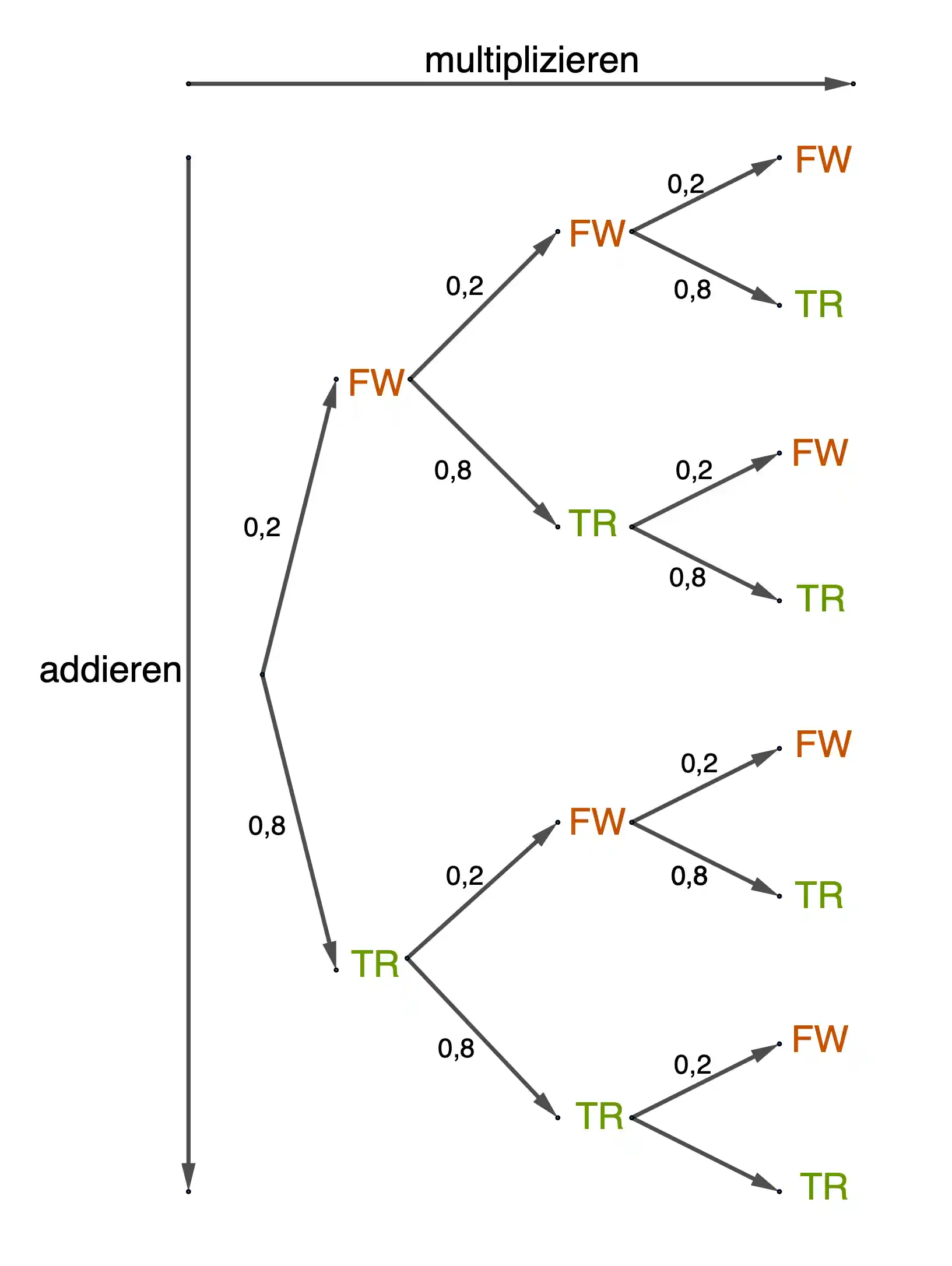
Viele verwechseln die Bernoulli-Formel mit normalen Aufgaben zur Wahrscheinlichkeit. Achte deshalb genau darauf, ob es sich um eine echte Bernoulli-Kette handelt. Ein häufiger Fehler ist auch, den falschen Wert für die Erfolgswahrscheinlichkeit einzusetzen – lies die Aufgabe immer sorgfältig. Tipp: Nutze die Formel nicht mechanisch, sondern versuche wirklich zu verstehen, was sie berechnet. Ein Baumdiagramm vorab hilft oft beim Einordnen. Und ganz wichtig: Prüfe, ob die Wahrscheinlichkeit für Erfolg und Misserfolg in jedem Durchlauf gleich bleibt.
Woher kommt die Bernoulli-Formel?
Die Formel geht zurück auf den Mathematiker Jakob Bernoulli, der im 17. Jahrhundert grundlegende Arbeiten zur Wahrscheinlichkeitsrechnung verfasste. Seine Untersuchungen zu wiederholten Zufallsexperimenten bildeten die Basis für das, was wir heute als Bernoulli-Kette und Bernoulli-Verteilung kennen. Sie zeigen, wie aus einfachen Ja-Nein-Versuchen mathematisch exakte Vorhersagen entstehen können – ein Konzept, das bis heute in der Statistik und in praktischen Anwendungen wie Qualitätskontrolle, Medizin und Informatik verwendet wird.
Moderne Anwendungen der Bernoulli-Formel
Auch heute ist die Bernoulli-Formel in vielen Bereichen relevant: in der Statistik, bei Umfragen, in der Technik und bei Testszenarien. Sie hilft überall dort, wo binäre Ereignisse auftreten – also z. B. beim Modellieren von Fehlerraten, beim Überprüfen von Produktqualität oder bei medizinischen Diagnosen. Besonders bei großen Datenmengen wird die Bernoulli-Formel oft als Teil komplexerer Modelle eingesetzt. Für Schülerinnen und Schüler bleibt sie aber ein klares und verständliches Werkzeug, um Wahrscheinlichkeiten bei wiederholten Versuchen zu bestimmen.
