Stochastik verstehen

Permutation – wie viele Möglichkeiten?

Lisa von OnMathe
two students high five

Überblick

Bei einer Permutation werden alle Objekte angeordnet. Dabei ist die Reihenfolge entscheidend.

Es gibt zwei typische Fälle – je nachdem, ob alle Objekte verschieden sind oder ob es identische gibt:

Permutation: Alle Objekte werden angeordnet
Formel Wann passt sie?
\( {\textcolor{orange}{n}}! \) Alle Objekte sind verschieden und die Reihenfolge ist wichtig.
\( \dfrac{{\textcolor{orange}{n}}!}{{\textcolor{green}{k_1}}!\cdot{\textcolor{green}{k_2}}!\cdot\dots} \) Einige Objekte sind identisch.

→ In Klassenarbeiten hilft dir diese Übersicht, schnell die richtige Formel zu wählen.

Wichtig
Eine Permutation zählt, wie viele verschiedene Anordnungen möglich sind, wenn alle Objekte verwendet werden.
→ Die Reihenfolge ist entscheidend.

Schauen wir uns beide Fälle jetzt Schritt für Schritt an – jeweils mit einem einfachen Beispiel.

Inhaltsverzeichnis

Das erwartet Dich

Überblick
Permutation - ohne Wiederholung
Permutation - mit Wiederholung
Abschlussbeispiel

Überblick

Bei einer Permutation werden alle Objekte angeordnet. Dabei ist die Reihenfolge entscheidend.

Es gibt zwei typische Fälle – je nachdem, ob alle Objekte verschieden sind oder ob es identische gibt:

Permutation: Alle Objekte werden angeordnet
Formel Wann passt sie?
\( {\textcolor{orange}{n}}! \) Alle Objekte sind verschieden und die Reihenfolge ist wichtig.
\( \dfrac{{\textcolor{orange}{n}}!}{{\textcolor{green}{k_1}}!\cdot{\textcolor{green}{k_2}}!\cdot\dots} \) Einige Objekte sind identisch.

→ In Klassenarbeiten hilft dir diese Übersicht, schnell die richtige Formel zu wählen.

Wichtig
Eine Permutation zählt, wie viele verschiedene Anordnungen möglich sind, wenn alle Objekte verwendet werden.
→ Die Reihenfolge ist entscheidend.

Schauen wir uns beide Fälle jetzt Schritt für Schritt an – jeweils mit einem einfachen Beispiel.

Permutation - ohne Wiederholung

Bei der Permutation ohne Wiederholung werden alle Objekte angeordnet – und jedes kommt genau einmal vor. Jede neue Reihenfolge zählt.
Sechs Läuferinnen laufen ein Rennen. Wie viele mögliche Ergebnisreihenfolgen gibt es?

Für den 1. Platz kommen 6 Läuferinnen infrage. Ist dieser vergeben, bleiben für den 2. Platz noch 5, für den 3. Platz 4 usw. – bis am Ende nur noch 1 Läuferin übrig ist.

Gesamtheit aller Objekte:
Läuferinnen → \( {\textcolor{orange}{n}} = {\textcolor{orange}{6}} \)
Alle Möglichkeiten multiplizieren:
\( {\textcolor{orange}{6}} \cdot {\textcolor{orange}{5}} \cdot {\textcolor{orange}{4}} \cdot {\textcolor{orange}{3}} \cdot {\textcolor{orange}{2}} \cdot {\textcolor{orange}{1}} = {\textcolor{midnightblue}{720}} \)
Kurzschreibweise (Fakultät):
\( {\textcolor{orange}{6}}! = {\textcolor{midnightblue}{720}} \)
  • insgesamt 6 Läuferinnen
  • alle sind verschieden (keine gleichen Objekte)
  • jede Läuferin kommt genau einmal vor
  • andere Reihenfolge → anderes Ergebnis

Es gibt also 720 verschiedene Reihenfolgen – also 720 mögliche Zieleinläufe im Rennen.

Merke
Bei der Permutation ohne Wiederholung sind alle Objekte verschieden und kommen genau einmal vor.
\( P = {\textcolor{orange}{n}}! \)
Fakultät
Das Ausrufezeichen hinter einer Zahl steht für die Fakultät.
Das bedeutet: Multipliziere die Zahl mit allen kleineren positiven Zahlen bis 1.
\( {\textcolor{orange}{n}}! = {\textcolor{orange}{n}} \cdot ({\textcolor{orange}{n}}-1) \cdot ({\textcolor{orange}{n}}-2) \cdot \dots \cdot {\textcolor{orange}{1}} \)
\( {\textcolor{orange}{4}}! = {\textcolor{orange}{4}} \cdot {\textcolor{orange}{3}} \cdot {\textcolor{orange}{2}} \cdot {\textcolor{orange}{1}} = {\textcolor{midnightblue}{24}} \)

Zum Abschluss ein kurzes weiteres Beispiel:

\( {\textcolor{orange}{5}} \) verschiedene Bücher sollen ins Regal gestellt werden.
\( P = {\textcolor{orange}{5}}! = \textcolor{midnightblue}{120} \)
→ Auch hier gilt: alle Objekte verschieden, Reihenfolge wichtig.

Jede Anordnung sofort richtig zählen: Das gelingt dir mit deinem Tutor.

Kostenlos testen: Mathe online lernen mit Nachhilfe von OnMathe

Permutation - mit Wiederholung

Bei der Permutation mit Wiederholung werden alle Objekte angeordnet – aber einige sind identisch. Vertauscht man gleiche Objekte, sieht das Ergebnis gleich aus.
Du hast 8 Bauklötze für einen Turm: 4 rote, 3 gelbe und 1 blauen Klotz. Auf wie viele verschiedene Weisen kannst du die Klötze stapeln?

An den untersten Platz kannst du einen von 8 Klötzen setzen. Danach bleiben 7, dann 6 … bis nur noch 1 übrig ist.

Aber: Einige Klötze sehen gleich aus - 4 rote, 3 gelbe und 1 blauer. Vertauscht man gleiche Klötze, entsteht kein neuer Turm.

Gesamtheit aller Objekte:
Klötze → \( {\textcolor{orange}{n}} = {\textcolor{orange}{8}} \)
Identische Gruppen:
\( {\textcolor{green}{k_1}} = {\textcolor{green}{4}} \) (rot), \( {\textcolor{green}{k_2}} = {\textcolor{green}{3}} \) (gelb), \( {\textcolor{green}{k_3}} = {\textcolor{green}{1}} \) (blau)
Allgemeine Formel:
\( P = \dfrac{{\textcolor{orange}{n}}!} {{\textcolor{green}{k_1}}! \cdot {\textcolor{green}{k_2}}! \cdot {\textcolor{green}{k_3}}! \dots} \)
Einsetzen:
\( P = \dfrac{{\textcolor{orange}{8}}!} {{\textcolor{green}{4}}! \cdot {\textcolor{green}{3}}! \cdot {\textcolor{green}{1}}!} \)
\( P = \dfrac{{\textcolor{midnightblue}{40320}}} {{\textcolor{midnightblue}{144}}} = {\textcolor{midnightblue}{280}} \)
  • insgesamt 8 Klötze
  • 4× rot, 3× gelb, 1× blau
  • gleiche Farben → nicht unterscheidbar
  • Vertauschen gleicher Klötze → keine neue Anordnung
  • Mehrfach gezählte Anordnungen müssen wir herausdividieren

Es gibt also 280 wirklich unterschiedliche Türme.

Merke
Bei der Permutation mit Wiederholung kommen einige Objekte mehrfach vor und sind nicht unterscheidbar.
\( P = \dfrac{{\textcolor{orange}{n}}!} {{\textcolor{green}{k_1}}! \cdot {\textcolor{green}{k_2}}! \cdot {\textcolor{green}{k_3}}! \dots} \)
\( {\textcolor{orange}{n}} \) ist die Gesamtanzahl aller Objekte. Die Werte \( {\textcolor{green}{k_1}}, {\textcolor{green}{k_2}}, {\textcolor{green}{k_3}}, \dots \) sind die Häufigkeiten der identischen Gruppen.

Zum Abschluss noch ein zweites schnelles Beispiel:

\( {\textcolor{orange}{6}} \) Kugeln sollen in einer Reihe angeordnet werden: \( {\textcolor{green}{3}} \) blau, \( {\textcolor{green}{2}} \) rot, \( {\textcolor{green}{1}} \) gelb.
\( {\textcolor{orange}{n}} = {\textcolor{orange}{6}} \quad {\textcolor{green}{k_1}} = {\textcolor{green}{3}} \quad {\textcolor{green}{k_2}} = {\textcolor{green}{2}} \quad {\textcolor{green}{k_3}} = {\textcolor{green}{1}} \)
\( P = \dfrac{{\textcolor{orange}{6}}!}{{\textcolor{green}{3}}!\cdot{\textcolor{green}{2}}!\cdot{\textcolor{green}{1}}!} \)
\( P = \dfrac{{\textcolor{midnightblue}{720}}}{{\textcolor{midnightblue}{12}}} = {\textcolor{midnightblue}{60}} \)
→ Es gibt 60 verschiedene Reihenfolgen.

Mit einem akademisch ausgebildeten Tutor verstehst du, warum man bei gleichen Objekten teilt.

Kostenlos testen: Online Mathe Nachhilfe bei OnMathe

Abschlussbeispiel

Zum Schluss zwei Aufgaben, bei denen du entscheiden musst: Liegt eine Permutation ohne Wiederholung oder eine Permutation mit Wiederholung vor?

Vier Freundinnen wollen sich für ein Foto nebeneinander aufstellen. Wie viele verschiedene Reihenfolgen sind möglich?
Alle Personen sind verschieden → ohne Wiederholung.
\( {\textcolor{orange}{n}} = {\textcolor{orange}{4}} \)
\( P = {\textcolor{orange}{n}}! = {\textcolor{orange}{4}}! \)
\( {\textcolor{orange}{4}}! = {\textcolor{orange}{4}} \cdot {\textcolor{orange}{3}} \cdot {\textcolor{orange}{2}} \cdot {\textcolor{orange}{1}} = {\textcolor{midnightblue}{24}} \)
→ Es gibt 24 verschiedene Reihenfolgen.
Betrachte die Ziffernfolge: \( 2, 3, 3, 5, 5, 5 \). Wie viele unterschiedliche Anordnungen sind möglich?
Einige Ziffern kommen mehrfach vor → mit Wiederholung.
\( {\textcolor{orange}{n}} = {\textcolor{orange}{6}} \) Ziffern
\( {\textcolor{green}{k_1}} = 1 \) (2), \( {\textcolor{green}{k_2}} = 2 \) (3), \( {\textcolor{green}{k_3}} = 3 \) (5)
Allgemeine Formel:
\( P = \dfrac{{\textcolor{orange}{n}}!} {{\textcolor{green}{k_1}}! \cdot {\textcolor{green}{k_2}}! \cdot {\textcolor{green}{k_3}}! \dots} \)
Einsetzen:
\( P = \dfrac{{\textcolor{orange}{6}}!} {{\textcolor{green}{1}}! \cdot {\textcolor{green}{2}}! \cdot {\textcolor{green}{3}}!} \)
\( P = \dfrac{{\textcolor{midnightblue}{720}}} {{\textcolor{midnightblue}{12}}} = {\textcolor{midnightblue}{60}} \)
→ Es gibt 60 verschiedene Anordnungen.

Kombinatorik macht Druck? Wir bringen Struktur.

Mathe macht Druck? Wir bringen Struktur.

Dein fester Tutor rechnet Permutationen mit dir, Schritt für Schritt.

Mathe-Nachhilfe online mit festem Tutor und Crashkurs vor jedem Test.

Mathe Nachhilfe online
Mathe Nachhilfe
Student lernt draußen im freien mit Notebook

Teste dein Wissen

Übungen

Sechs Schülerinnen stellen sich für ein Klassenfoto in einer Reihe auf. Wie viele verschiedene Aufstellungen sind möglich?

Lösung

Es werden alle \( 6 \) Personen verwendet und jede kommt genau einmal vor → Permutation ohne Wiederholung.
\( {\textcolor{orange}{n}} = 6 \Rightarrow P = {\textcolor{orange}{n}}! = 6! = 720 \)

Aus den Buchstaben des Wortes „MAMA“ sollen alle möglichen verschiedenen Anordnungen gebildet werden. Wie viele unterschiedliche „Wörter“ entstehen?

Lösung

Insgesamt \( 4 \) Buchstaben, davon \( 2 \) mal \( M \) und \( 2 \) mal \( A \) → Permutation mit Wiederholung.
\( {\textcolor{orange}{n}} = 4 \Rightarrow P = \dfrac{4!}{2! \cdot 2!} = \dfrac{24}{4} = 6 \)

Ausgewählt für Dich

Empfohlene Beiträge

Bernoulli-Ketten erkennen, Formel einsetzen, Wahrscheinlichkeiten berechnen – ganz ohne Panik.

Die Bernoulli-Formel: Grundlagen der Binomialverteilung

Bernoulli-Ketten erkennen, Formel einsetzen, Wahrscheinlichkeiten berechnen – ganz ohne Panik.

Kombinatorik verständlich erklärt: So erkennst du Permutation, Variation und Kombination sicher und findest die richtige Formel

Kombinatorik Formeln

Kombinatorik verständlich erklärt: So erkennst du Permutation, Variation und Kombination sicher und findest die richtige Formel

Binomialverteilung einfach erklärt - Mit Beispielen, Histogrammen und Tipps zur Taschenrechner-Anwendung.

Die Binomialverteilung – mit Formel & Beispielen

Binomialverteilung einfach erklärt - Mit Beispielen, Histogrammen und Tipps zur Taschenrechner-Anwendung.

Mehr dazu

in unseren FAQs

Woran erkenne ich schnell, ob ich „mit“ oder „ohne Wiederholung“ rechnen muss?

Wenn jedes Objekt einzigartig ist → ohne Wiederholung: \( {\textcolor{orange}{n}}! \)
Wenn Objekte gleich aussehen → mit Wiederholung: \( P = \dfrac{{\textcolor{orange}{n}}!} {{\textcolor{green}{k_1}}! \cdot {\textcolor{green}{k_2}}! \dots} \)

Warum muss man bei Wiederholung durch die Fakultäten der Gruppen teilen?

Gleiche Objekte erzeugen keine neuen Anordnungen.
Durch das Dividieren entfernst du alle Varianten, die optisch identisch sind.

Was bedeutet die Fakultät überhaupt?

Die Fakultät \( {\textcolor{orange}{n}}! \) zählt alle Reihenfolgen, wenn jedes Objekt genau einmal vorkommt.
\( {\textcolor{orange}{5}}! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = {\textcolor{midnightblue}{120}} \)

Muss ich die Objekte immer komplett verwenden?

Ja. Bei Permutationen werden immer alle Plätze gefüllt und alle Objekte genutzt.
Wenn du nur einige auswählst, bist du bei Kombinationen oder Variationen.

Was ist der häufigste Fehler bei Permutationen?

Viele starten sofort mit \( n\! \), ohne zu prüfen, ob es identische Objekte gibt.
→ Erst unterscheiden, ob Wiederholung vorliegt, dann die passende Formel wählen.

Mehr dazu

Weiterführende Informationen

Ohne vs. mit Wiederholung – der Vergleich

Jetzt weißt du, wie beide Arten der Permutation funktionieren. In dieser Übersicht siehst du noch einmal, wann du welche Variante verwendest.

ohne Wiederholung mit Wiederholung
Bedeutung Jedes Objekt wird nur einmal verwendet. Manche Objekte wiederholen sich oder sehen gleich aus.
Beispiel 6 Läuferinnen in einem Rennen – jede belegt einen anderen Platz. 8 Bauklötze mit gleichen Farben – vertauschte gleiche Klötze ergeben kein neues Ergebnis.
Formel \( P = {\textcolor{orange}{n}}! \) \( P = \dfrac{{\textcolor{orange}{n}}!} {{\textcolor{green}{k_1}}! \cdot {\textcolor{green}{k_2}}! \cdot {\textcolor{green}{k_3}}! \dots} \)
Typischer Gedanke „Ich verwende jedes Teil genau einmal.“ „Einige Teile sind gleich – ich muss sie nicht doppelt zählen.“
ohne Wiederholung mit Wiederholung
Bedeutung:
Jedes Objekt wird nur einmal verwendet. 		Bedeutung:
Manche Objekte wiederholen sich oder sehen gleich aus.
Beispiel:
6 Läuferinnen – jede belegt einen anderen Platz. 		Beispiel:
8 Bauklötze mit gleichen Farben – vertauschte gleiche Klötze ergeben kein neues Ergebnis.
Formel:
\( P = {\textcolor{orange}{n}}! \) 		Formel:
\( P = \dfrac{{\textcolor{orange}{n}}!} {{\textcolor{green}{k_1}}! \cdot {\textcolor{green}{k_2}}! \cdot {\textcolor{green}{k_3}}! \dots} \)
Typischer Gedanke:
„Ich verwende jedes Teil genau einmal.“ 		Typischer Gedanke:
„Einige Teile sind gleich – ich muss sie nicht doppelt zählen.“

Kurz gesagt: ohne Wiederholung nutzt du die einfache Fakultät \( {\textcolor{orange}{n}}! \). Bei Wiederholung startest du ebenfalls mit \( {\textcolor{orange}{n}}! \), teilst aber durch die Fakultäten der identischen Gruppen.

Merke
Prüfe immer zuerst: Kommen Objekte doppelt vor?
• alle Objekte verschieden → \( P = {\textcolor{orange}{n}}! \)
• einige Objekte gleich
→ \( P = \dfrac{{\textcolor{orange}{n}}!} {{\textcolor{green}{k_1}}! \cdot {\textcolor{green}{k_2}}! \cdot {\textcolor{green}{k_3}}! \dots} \)

Die Formel verstehen

Die Formel für Permutationen mit Wiederholung kennst du bereits – jetzt zeigen wir dir, warum sie so aussieht.

Wichtig
• alle Objekte werden verwendet
• einige Objekte sind identisch
• gleiche Objekte → ergeben dieselbe Anordnung
Du hast 8 Klötze: 4 rot, 3 gelb, 1 blau. Wie viele verschiedene Türme kannst du bauen?

Baust du den Turm Stein für Stein, hast du zuerst 8 Möglichkeiten, dann 7, dann 6 … bis der letzte Platz mit 1 Klotz gefüllt wird.

Anzahl Möglichkeiten zu bauen:
\( {\textcolor{orange}{8}} \cdot {\textcolor{orange}{7}} \cdot {\textcolor{orange}{6}} \cdot {\textcolor{orange}{5}} \cdot {\textcolor{orange}{4}} \cdot {\textcolor{orange}{3}} \cdot {\textcolor{orange}{2}} \cdot {\textcolor{orange}{1}} = {\textcolor{midnightblue}{40320}} \)
→ Das ist die Fakultät \( {\textcolor{orange}{8}}! \)
  • insgesamt 8 Klötze → \( {\textcolor{orange}{8}}! \) Möglichkeiten
  • Aber: 4× rot, 3× gelb, 1× blau
  • gleiche Farben → nicht unterscheidbar
  • Vertauschen gleicher Klötze → keine neue Anordnung, der Turm sieht immer gleich aus.
Vertauschungen, die den Turm nicht verändern:
  • \( {\textcolor{green}{4}}! \) → rote Klötze
  • \( {\textcolor{green}{3}}! \) → gelbe Klötze
  • \( {\textcolor{green}{1}}! \) → blauer Klotz
Gesamt: \( {\textcolor{green}{4}}! \cdot {\textcolor{green}{3}}! \cdot {\textcolor{green}{1}}! \)

Alles, was den Turm optisch nicht verändern, müssen wir aus der Gesamtzahl herausnehmen. Das machen wir, indem wir durch all diese Vertauschungen dividieren.

Gesamtzahl aller Objekte:
\( {\textcolor{orange}{n}} = {\textcolor{orange}{8}} \)
Identische Gruppen:
\( {\textcolor{green}{k_1}} = {\textcolor{green}{4}} \) (rot), \( {\textcolor{green}{k_2}} = {\textcolor{green}{3}} \) (gelb), \( {\textcolor{green}{k_3}} = {\textcolor{green}{1}} \) (blau)
Allgemeine Formel:
\( P = \dfrac{{\textcolor{orange}{n}}!} {{\textcolor{green}{k_1}}! \cdot {\textcolor{green}{k_2}}! \cdot {\textcolor{green}{k_3}}! \dots} \)
Einsetzen:
\( P = \dfrac{{\textcolor{orange}{8}}!} {{\textcolor{green}{4}}! \cdot {\textcolor{green}{3}}! \cdot {\textcolor{green}{1}}!} \)
\( P = \dfrac{{\textcolor{midnightblue}{40320}}} {{\textcolor{midnightblue}{144}}} = {\textcolor{midnightblue}{280}} \)

Ergebnis: 280 unterschiedliche Türme – alle anderen wären optisch gleich.

Merke
Bei der Permutation mit Wiederholung startest du mit \( {\textcolor{orange}{n}}! \) und entfernst alle Anordnungen, die sich durch identische Objekte nicht unterscheiden.
\( P = \dfrac{{\textcolor{orange}{n}}!} {{\textcolor{green}{k_1}}! \cdot {\textcolor{green}{k_2}}! \cdot {\textcolor{green}{k_3}}! \dots} \)
\( {\textcolor{orange}{n}} \) = Gesamtzahl aller Objekte
\( {\textcolor{green}{k_i}} \) = Häufigkeiten der identischen Gruppen

Permutation im Alltag – zwei Beispiele

Du begegnest Permutationen ständig im Alltag. Besonders dann, wenn die Reihenfolge etwas verändert oder festlegt. Diese zwei Beispiele zeigen dir, wo Permutationen vorkommen.

Deine Musik läuft im Shuffle-Modus.
Stell dir vor, du hast eine Playlist mit 12 verschiedenen Songs. Im Shuffle werden alle Songs genau einmal gespielt – aber in immer anderer Reihenfolge.
Wie viele unterschiedliche Reihenfolgen gibt es?
\( {\textcolor{orange}{12}}! = {\textcolor{midnightblue}{479001600}} \)
→ Es gibt über 479 Millionen mögliche Abspielfolgen.

Wenn ein Song 3 Minuten dauert, bräuchtest du 2 730 000 000 Minuten, um alle Reihenfolgen einmal zu hören. Das sind über 5000 Jahre – verdammt lange, oder?

Warum passt das hier?
• alle Songs sind verschieden
• jeder Song kommt genau einmal vor
• Reihenfolge ändert das Ergebnis → klassische Permutation
Dein Bruder sortiert deine Sneaker um.
Er stellt sie neu in deinem Regal auf – in einer einzigen Reihe.
  • 3 gleiche weiße Sneaker
  • 2 gleiche schwarze Sneaker
  • 1 besonderes Modell (nur einmal vorhanden)
Wie viele verschiedene Reihenfolgen könnte er gebaut haben?

Insgesamt hast du 6 Sneaker. Wären alle verschieden, gäbe es \( {\textcolor{orange}{6}}! = {\textcolor{midnightblue}{720}} \) mögliche Reihenfolgen.

Alle theoretischen Reihenfolgen:
\( {\textcolor{orange}{6}}! = {\textcolor{orange}{6}} \cdot {\textcolor{orange}{5}} \cdot {\textcolor{orange}{4}} \cdot {\textcolor{orange}{3}} \cdot {\textcolor{orange}{2}} \cdot {\textcolor{orange}{1}} = {\textcolor{midnightblue}{720}} \)

Aber: Die weißen Sneaker sehen gleich aus – und die schwarzen auch. Vertauschst du gleiche Schuhe, ändert sich die Reihenfolge optisch nicht.

Vertauschungen, die das Ergebnis nicht verändern:
  • \( {\textcolor{green}{3}}! \) → weiße Sneaker
  • \( {\textcolor{green}{2}}! \) → schwarze Sneaker
  • \( {\textcolor{green}{1}}! \) → der besondere Sneaker
Gesamt: \( {\textcolor{green}{3}}! \cdot {\textcolor{green}{2}}! \cdot {\textcolor{green}{1}}! \)

Diese „überzähligen“ Varianten müssen wir aus der Gesamtzahl entfernen – also teilen wir durch diese Vertauschungen.

Allgemeine Formel:
\( P = \dfrac{{\textcolor{orange}{n}}!} {{\textcolor{green}{k_1}}! \cdot {\textcolor{green}{k_2}}! \cdot {\textcolor{green}{k_3}}! \dots} \)
Einsetzen:
\( P = \dfrac{{\textcolor{orange}{6}}!} {{\textcolor{green}{3}}! \cdot {\textcolor{green}{2}}! \cdot {\textcolor{green}{1}}!} \)
\( P = \dfrac{{\textcolor{midnightblue}{720}}} {{\textcolor{midnightblue}{12}}} = {\textcolor{midnightblue}{60}} \)

Es gibt also 60 verschiedene Anordnungen, die dein Bruder gebaut haben könnte. Wenn er das alles wirklich ausprobiert hat … dann hatte er eindeutig zu viel Zeit. 😉

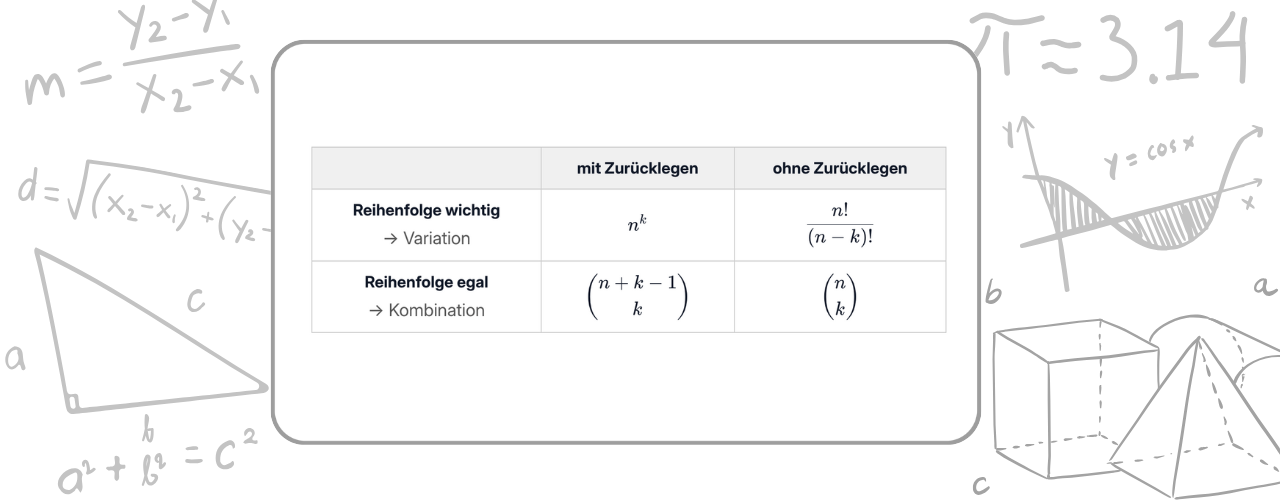
Grenzen der Permutation – und wie es in der Kombinatorik weitergeht

Permutationen sind ein starkes Werkzeug, wenn du alle Objekte verwendest und die Reihenfolge entscheidend ist. Doch es gibt Situationen, in denen diese Idee nicht mehr ausreicht. Genau hier beginnt der Rest der Kombinatorik.

Wichtig
Permutation passt nur, wenn alle Objekte benutzt werden.
Sobald du nur einen Teil auswählst oder die Reihenfolge egal ist, brauchst du andere Werkzeuge.

Die typischen Fälle, in denen Permutationen an ihre Grenzen stoßen:

  • Du verwendest nicht alle Objekte.
    Beispiel: Aus 10 Büchern sollen nur 3 ausgewählt und angeordnet werden.
    → Das ist keine Permutation mehr, sondern eine Variation.
  • Die Reihenfolge spielt keine Rolle.
    Beispiel: Du stellst ein Team aus 5 Personen zusammen – egal, wer links oder rechts steht.
    → Das ist eine Kombination.
  • Es wird gezogen mit Zurücklegen.
    Beispiel: Du ziehst mehrmals farbige Kugeln aus einer Box, aber legst jede Kugel wieder zurück.
    → Auch das ist keine Permutation – hier ändern sich die Regeln komplett.

Du merkst: Permutationen sind nur der erste Schritt der Kombinatorik. Sobald sich Auswahlgröße oder Reihenfolge ändern, brauchst du neue Formeln – zum Beispiel die Variation oder die Kombination.

Du willst wissen, wie man auswählt, ohne alles anzuordnen? Dann schau dir unseren Beitrag Kombinatorik Formeln an.

Vertiefung

Warum die Permutation der Startpunkt der Kombinatorik ist

Die Permutation ist kein Spezialfall – sie ist der Grundgedanke der gesamten Kombinatorik. Hier wird zum ersten Mal gezählt, wie viele verschiedene Anordnungen möglich sind, wenn wirklich alles verwendet wird.

Bei einer Permutation wird nichts ausgewählt und nichts weggelassen.
→ Es geht ausschließlich um die Reihenfolge.

Genau deshalb taucht hier zum ersten Mal die Fakultät auf:

\( {\textcolor{orange}{n}}! = {\textcolor{orange}{n}} \cdot ({\textcolor{orange}{n}}-1) \cdot \dots \cdot 1 \)

Diese Rechnung entsteht nicht zufällig: Für den ersten Platz gibt es noch n Möglichkeiten, für den zweiten nur noch n−1 usw.

Jede neue Position reduziert die Auswahl – bis am Ende nur noch eine Möglichkeit bleibt.

Viele typische Fehler in Klassenarbeiten entstehen genau hier:

Häufiger Denkfehler
Schülerinnen und Schüler verwenden eine Permutation, obwohl nicht alle Objekte genutzt werden.
→ Dann ist es keine Permutation, sondern eine andere Zählmethode.

Darum ist die Permutation so wichtig: Sie ist der Vergleichsmaßstab für alle weiteren Fälle.

• Permutation: alle Objekte, Reihenfolge wichtig
• Variation: nicht alle Objekte, Reihenfolge wichtig
• Kombination: nicht alle Objekte, Reihenfolge egal
Merke
Die Permutation beantwortet immer die Frage:
„In wie vielen verschiedenen Reihenfolgen lassen sich alle Objekte anordnen?“
Permutation ist ein Teil der Kombinatorik. Wenn du das Thema ganz verstehen willst – inklusive Variation und Kombination – findest du hier den kompletten Überblick.
Gratis Probestunde sichern
OnMathe
Deine Bildung, unsere Mission – made with ☕️ in Baden-Württemberg
Kontakt
Montag–Freitag
13:00–18:30 Uhr
07321 75899-39
Jobs
BenefitsJetzt bewerben
Social
© 2026 OnMathe. Alle Rechte vorbehalten.
DatenschutzImpressumCookie-Einstellungen