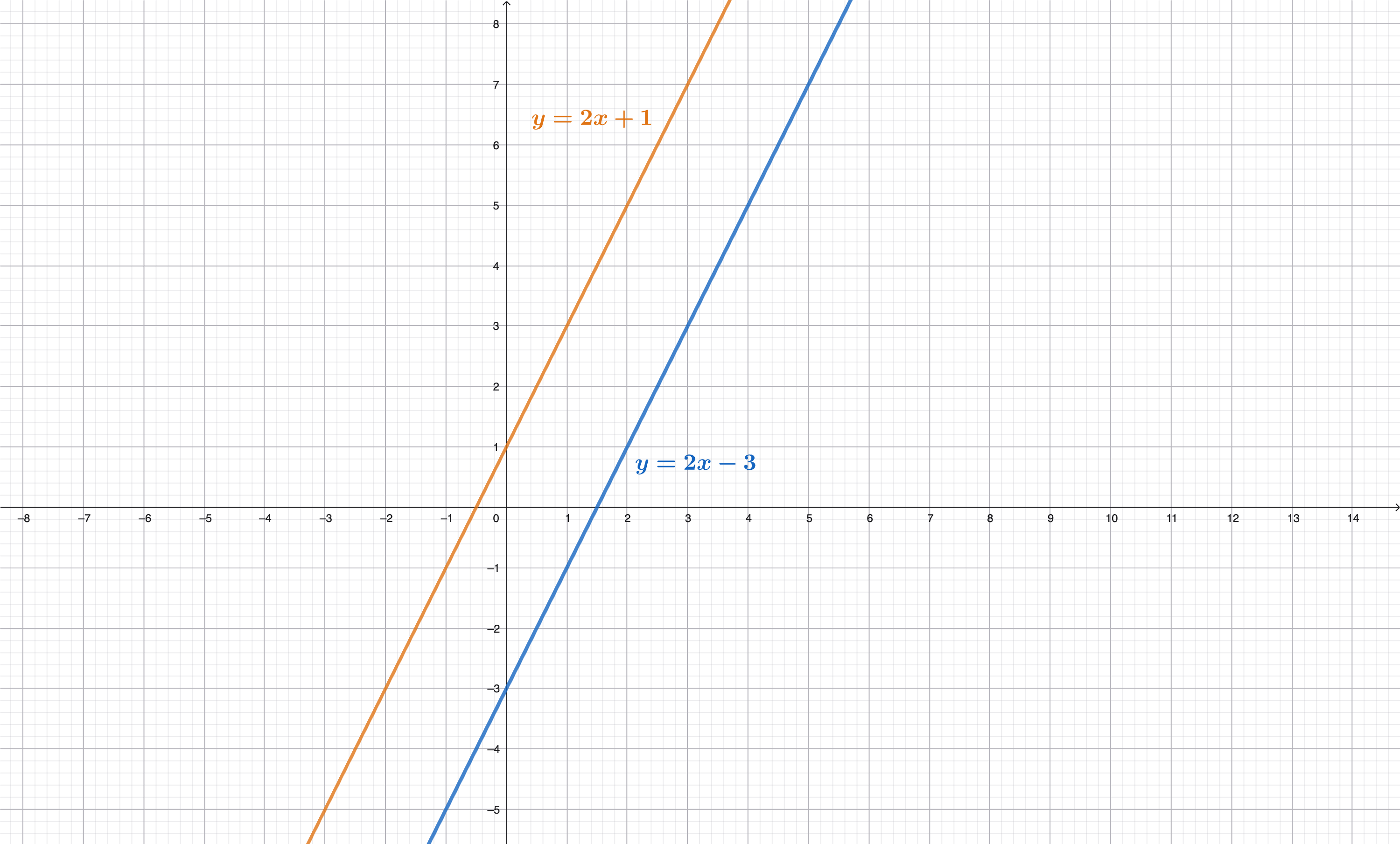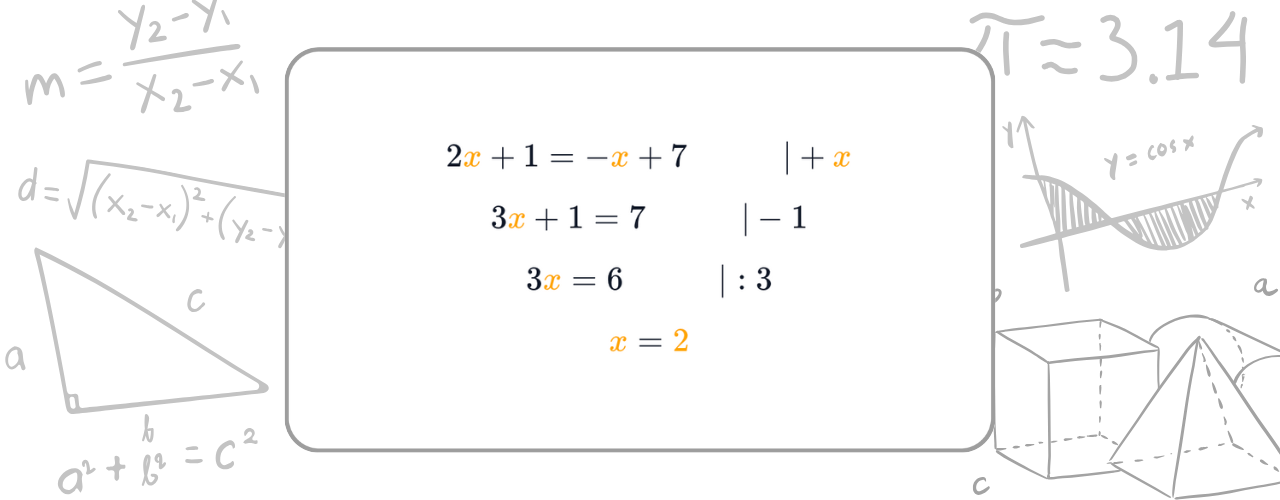Eine, keine oder unendlich viele Lösungen erkennen
lineare Gleichungssysteme zeichnerisch lösen
Einleitung
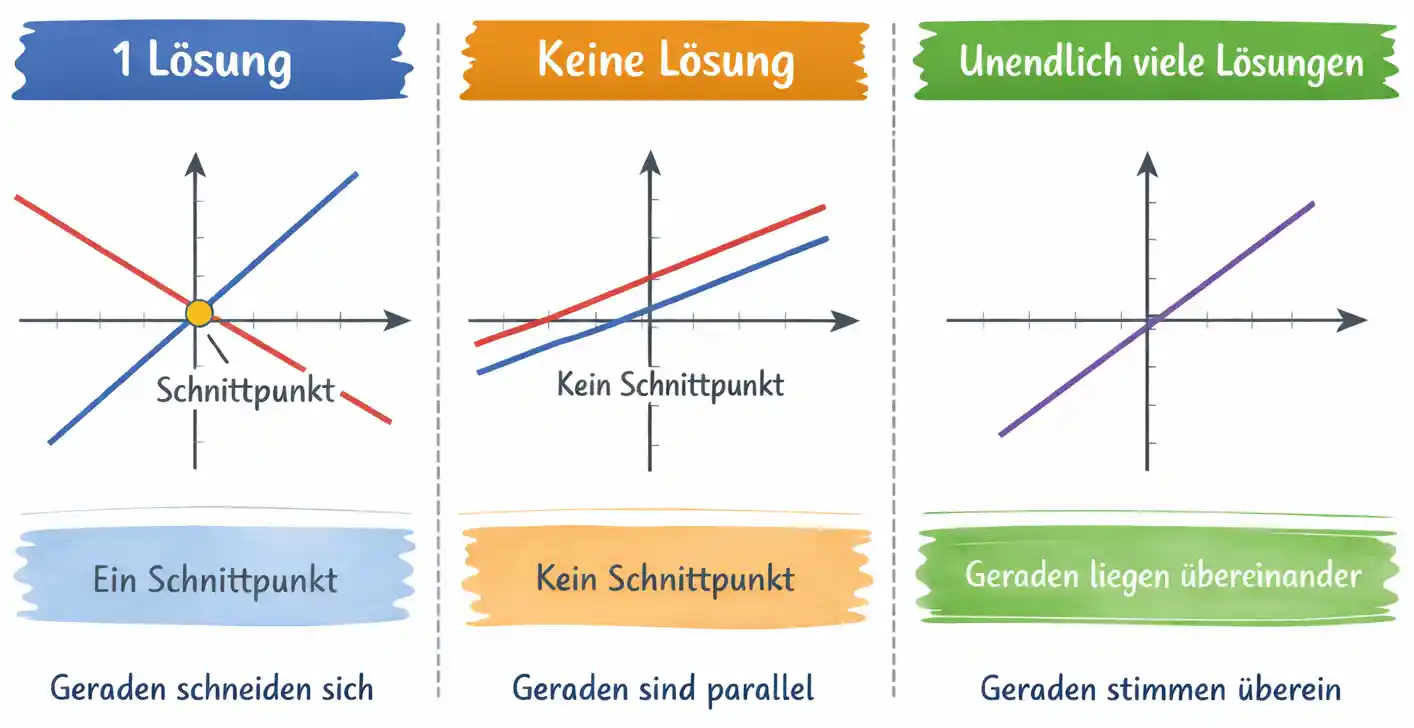
Ein lineares Gleichungssystem kann eine, keine oder auch unendlich viele Lösungen haben. Warum das so ist, wird sofort klar, wenn wir es uns grafisch anschauen:
-
Unterschiedliche Steigungen
→ genau eine Lösung -
Gleiche Steigung, unterschiedlicher y-Achsenabschnitt
→ keine Lösung -
Gleiche Steigung, gleicher y-Achsenabschnitt
→ unendlich viele Lösungen
Die eindeutige Lösung eines LGS ist der Schnittpunkt der beiden Geraden.
Du kannst das LGS grafisch lösen, indem du den Schnittpunkt abliest.
Einleitung
Ein lineares Gleichungssystem kann eine, keine oder auch unendlich viele Lösungen haben. Warum das so ist, wird sofort klar, wenn wir es uns grafisch anschauen:
-
Unterschiedliche Steigungen
→ genau eine Lösung -
Gleiche Steigung, unterschiedlicher y-Achsenabschnitt
→ keine Lösung -
Gleiche Steigung, gleicher y-Achsenabschnitt
→ unendlich viele Lösungen
Die eindeutige Lösung eines LGS ist der Schnittpunkt der beiden Geraden.
Du kannst das LGS grafisch lösen, indem du den Schnittpunkt abliest.
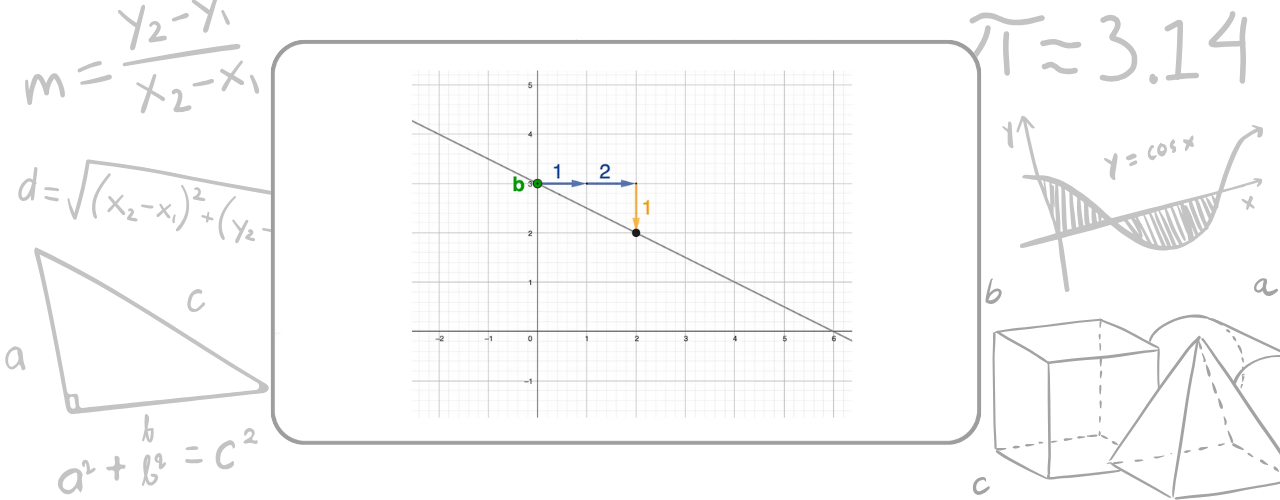
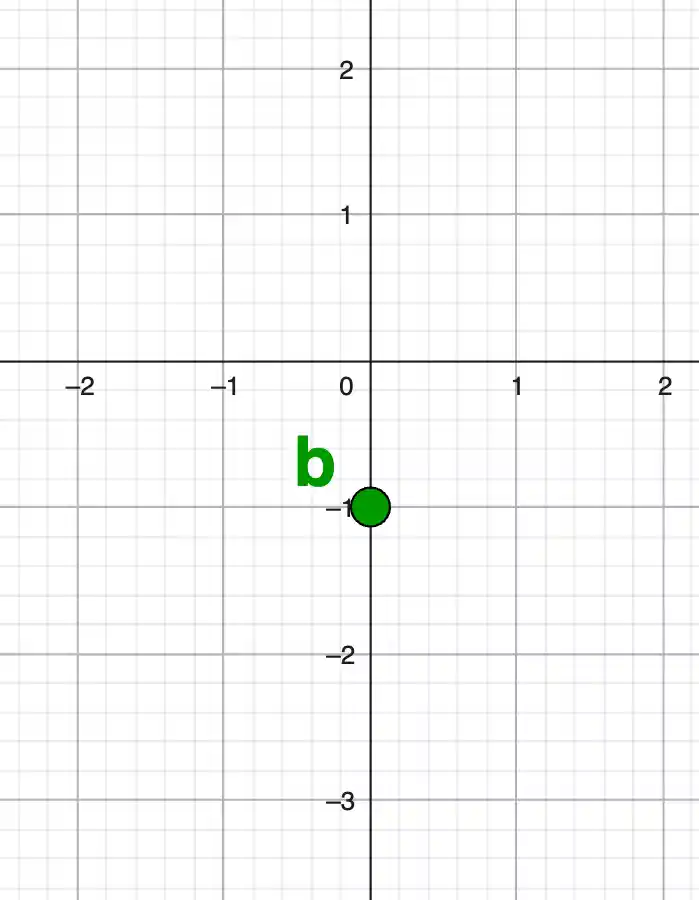
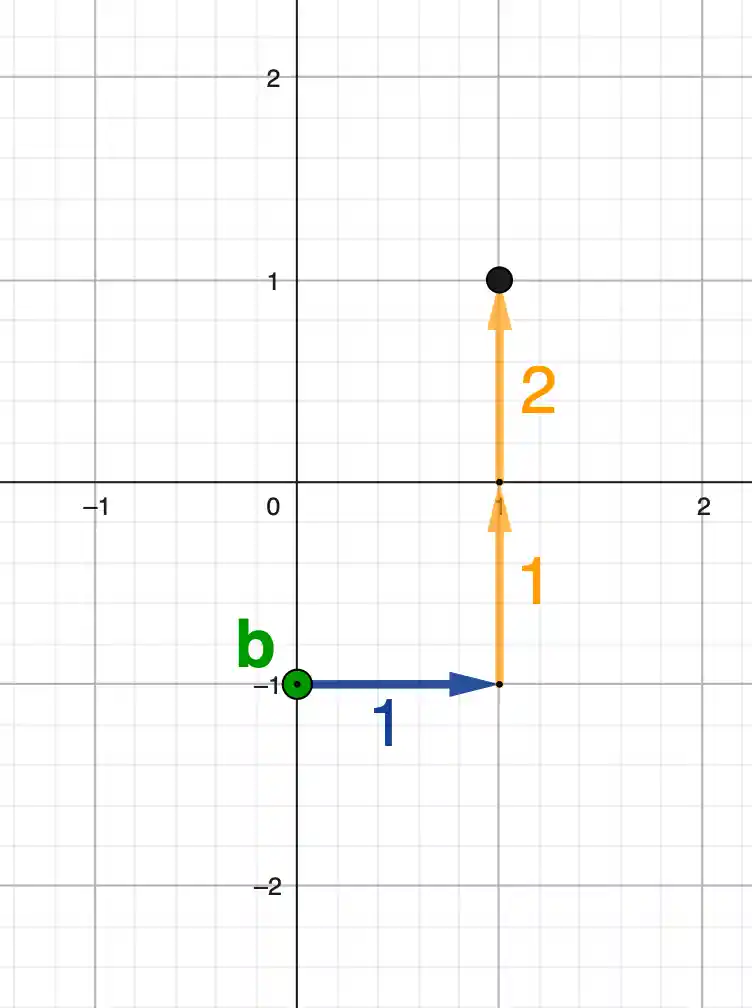
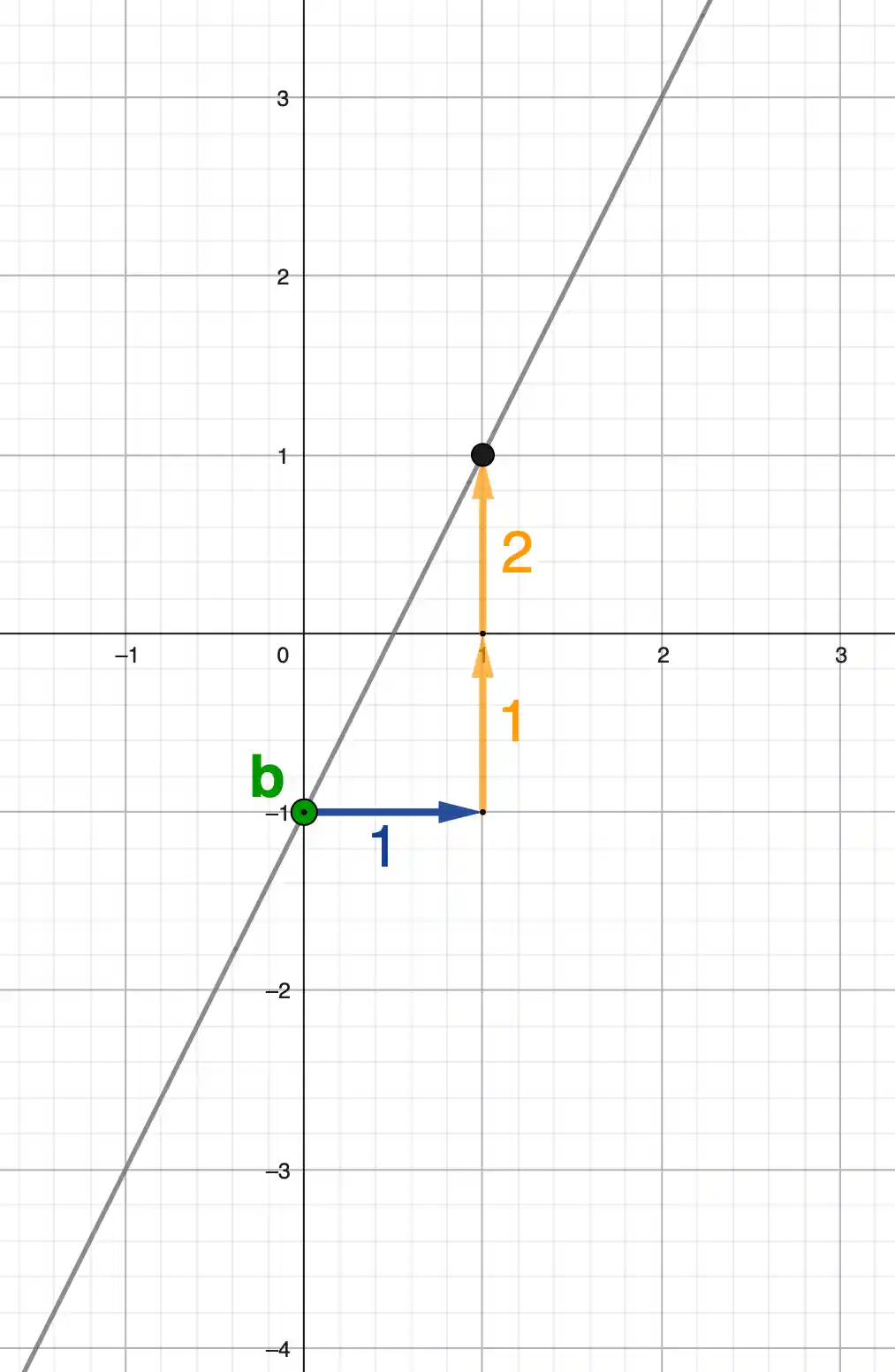
LGS zeichnerisch lösen
Ein lineares Gleichungssystem kann man auch zeichnerisch lösen. Dabei werden beide Gleichungen als Geraden ins Koordinatensystem gezeichnet.
keine Lösung
Nicht jedes lineare Gleichungssystem hat eine Lösung. Manchmal schneiden sich die Geraden gar nicht.
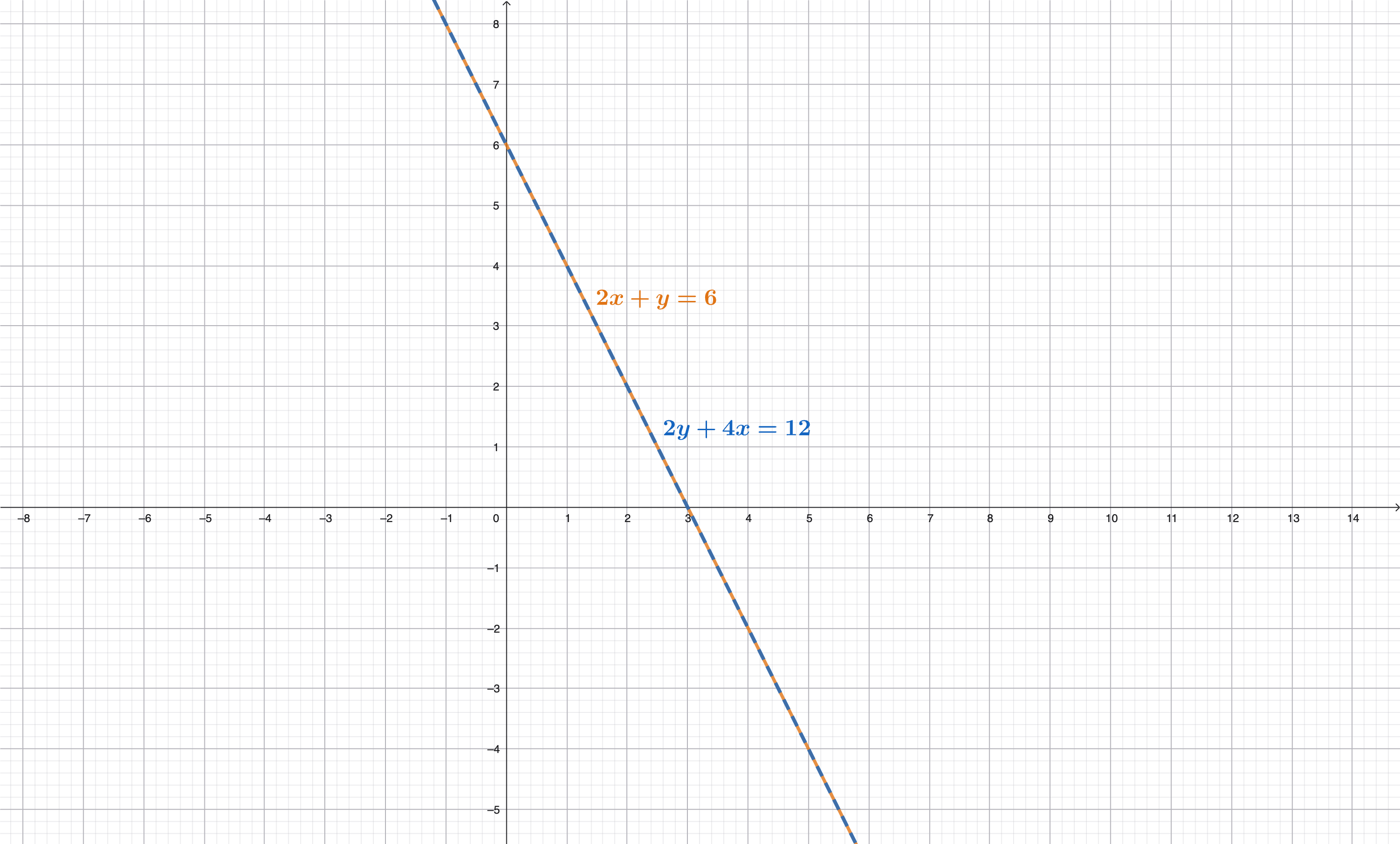
unendlich Lösungen
Manchmal hat ein lineares Gleichungssystem unendlich viele Lösungen. Dann liegen beide Geraden genau übereinander.
Wenn du beide Gleichungen in die Form \(y = mx + b\) bringst, kommt dieselbe Gerade heraus.
→ Es gibt unendlich viele Lösungen (alle Punkte auf der Geraden).
→ gleicher y-Achsenabschnitt
Du suchst Profi-Nachhilfe mit echtem Impact? Dann bist du bei OnMathe genau richtig!
Verstehe Mathe ab der ersten Stunde.

Teste dein Wissen
Übungen
Lösung
Lösung
Lösung
Ausgewählt für Dich
Empfohlene Beiträge
Mehr dazu
in unseren FAQs
Wann kann ich ein lineares Gleichungssystem zeichnerisch lösen?
Was ist beim Zeichnen die Lösung des LGS?
Was bedeutet es, wenn sich die Geraden nicht schneiden?
Woran erkenne ich zeichnerisch unendlich viele Lösungen?
Ist das zeichnerische Lösen immer exakt?
Mehr dazu
Weiterführende Informationen
Lineare Funktionen zeichnen
Um ein lineares Gleichungssystem grafisch zu lösen, musst du die zugehörigen Geraden zeichnen. Dafür müssen die Gleichungen in der Form \( y = mx + b \) vorliegen.
rechnerische Lösungsverfahren
Ein lineares Gleichungssystem kann nicht nur grafisch, sondern auch rechnerisch gelöst werden. Dafür gibt es drei Verfahren: Einsetzungsverfahren, Gleichsetzungsverfahren und Additionsverfahren.
Hier siehst du alle drei Verfahren kompakt an je einem Beispiel.
Einsetzungsverfahren
Gleichsetzungsverfahren
Additionsverfahren
Wann nutze ich was?
In Textaufgaben ist nicht das Rechnen das Problem, sondern das passende Verfahren zu finden. Hier siehst du typische Aufgaben – jeweils mit kurzer Beispielrechnung.
Einsetzungsverfahren
Zusammen sind sie 28 Jahre alt.
Gleichsetzungsverfahren
Additionsverfahren
Ein Erwachsenenticket kostet 7 Euro, ein Kinderticket 5 Euro.
Insgesamt wurden 117 Euro eingenommen.
Nerdecke
Ein lineares Gleichungssystem beschreibt nicht nur eine Rechenaufgabe, sondern immer auch eine geometrische Situation.
Jede lineare Gleichung steht für eine Gerade im Koordinatensystem. Ein Gleichungssystem verknüpft diese Geraden miteinander.
Zwei Geraden können sich im Koordinatensystem nur auf drei grundsätzlich verschiedene Arten zueinander verhalten.
Schneiden sich die Geraden, existiert genau ein gemeinsamer Punkt. Das Gleichungssystem ist dann eindeutig lösbar.
Verlaufen die Geraden parallel, haben sie keinen gemeinsamen Punkt. Das Gleichungssystem ist dann unlösbar.
Fallen beide Geraden zusammen, bestehen unendlich viele gemeinsame Punkte. In diesem Fall besitzt das Gleichungssystem unendlich viele Lösungen.
Rechnerische Lösungsverfahren wie Einsetzen, Gleichsetzen oder Addieren führen immer zu genau demselben Ergebnis, das man auch grafisch erkennen würde.
Widersprüche in der Rechnung (zum Beispiel \( 0 = 5 \)) entsprechen grafisch parallelen Geraden.
Identische Gleichungen entsprechen grafisch deckungsgleichen Geraden und erklären, warum es dann unendlich viele Lösungen gibt.
Auch wenn lineare Gleichungssysteme meist rechnerisch gelöst werden, liefert die grafische Betrachtung wichtige Informationen, die man in der Rechnung nicht sofort sieht.
Sie zeigt:
• wie viele Lösungen es gibt
• warum ein Verfahren funktioniert oder scheitert
Deshalb wird das zeichnerische Lösen häufig genutzt, um Ergebnisse zu kontrollieren oder Lösungswege besser zu verstehen.

13:00 -18:30 Uhr
5 von 5 Sternen auf Google