Funktionen verstehen
lineare Funktionen
Einleitung
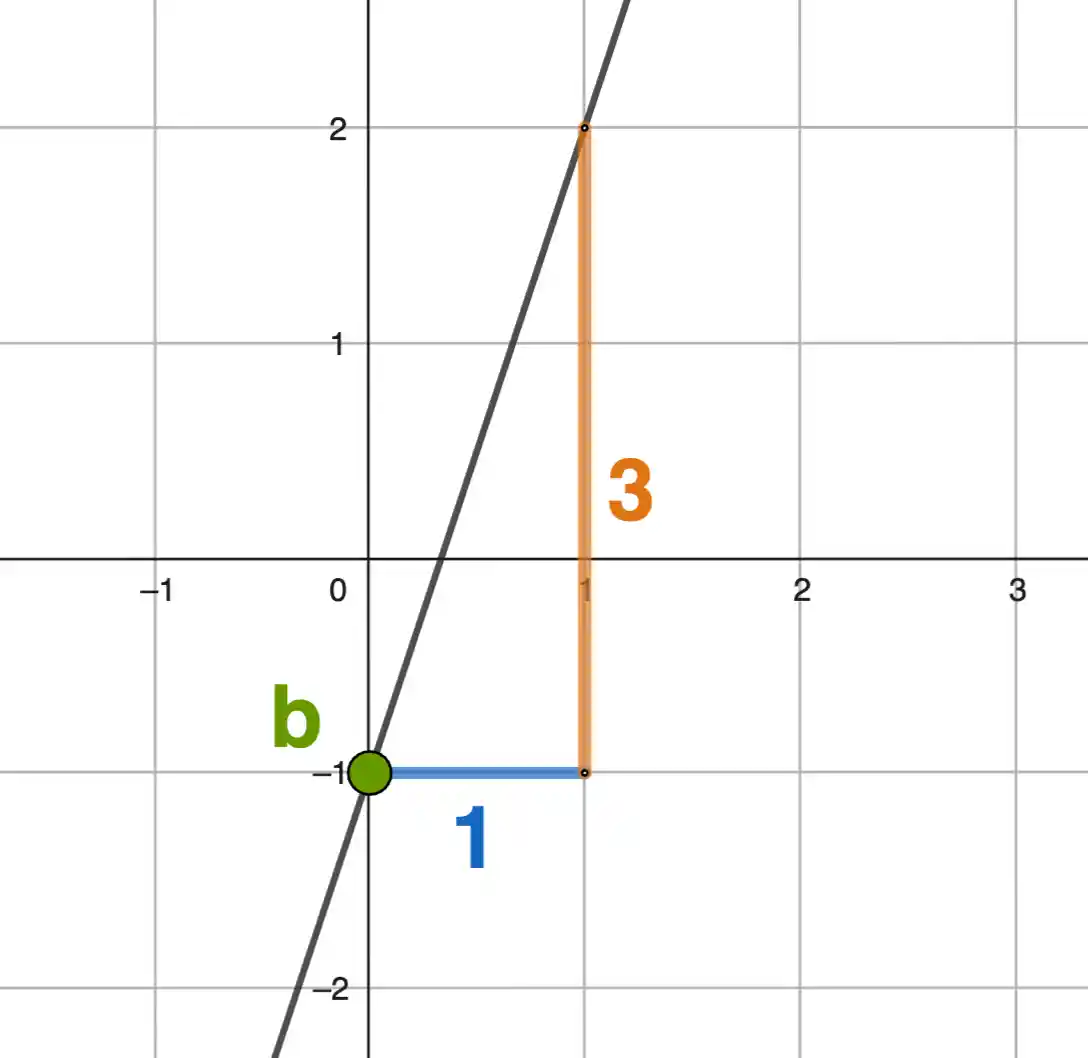
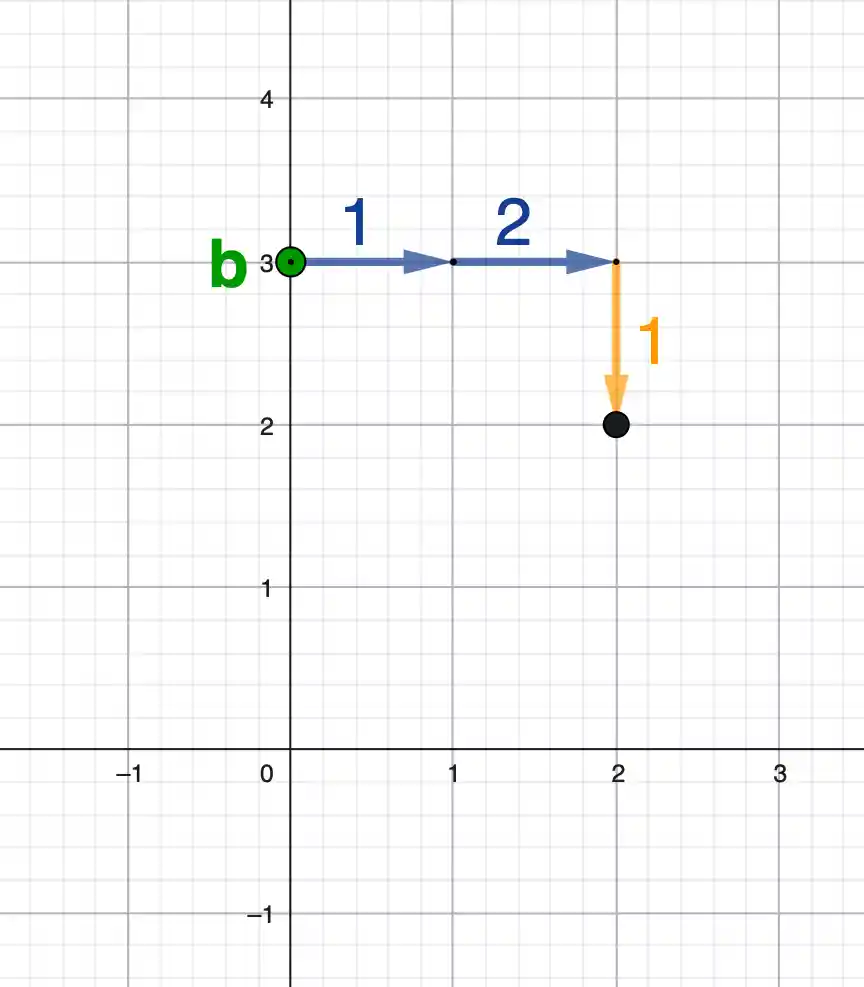
Mit einer linearen Funktion beschreibst du eine Gerade. Wie das aussieht und wie du sie zeichnest, siehst du direkt am Beispiel:
\( f(x) = {\textcolor{orangered}{3}}x - {\textcolor{green}{1}} \)
Startpunkt: \( (0|{\textcolor{green}{-1}}) \)
Steigung:
\( {\textcolor{orangered}{m}} =
\dfrac{{\textcolor{orange}{3}}}{{\textcolor{blue}{1}}} \)
→ \( {\textcolor{blue}{1}} \) nach rechts,
\( {\textcolor{orange}{3}} \) nach oben
Startpunkt markieren, Steigung laufen, Gerade zeichnen.
Das übst du im Beitrag Schritt für Schritt mit Aufgaben.
Merke
Eine lineare Funktion hat immer die Form:
\( f(x) = {\textcolor{orangered}{m}} \cdot x + {\textcolor{green}{b}} \)
- \( {\textcolor{green}{b}} \): Startpunkt auf der y-Achse → Punkt \( (0|{\textcolor{green}{b}}) \)
- \( {\textcolor{orangered}{m}} \): Steigung → als Bruch denken:
- \( \dfrac{\textcolor{orange}{Zähler}}{\textcolor{midnightblue}{Nenner}} \) → \({\textcolor{midnightblue}{Nenner}}\) nach rechts, \({\textcolor{orange}{Zähler}}\) nach oben
- Nur bei negativem \( {\textcolor{orangered}{m}} \): nach unten gehen
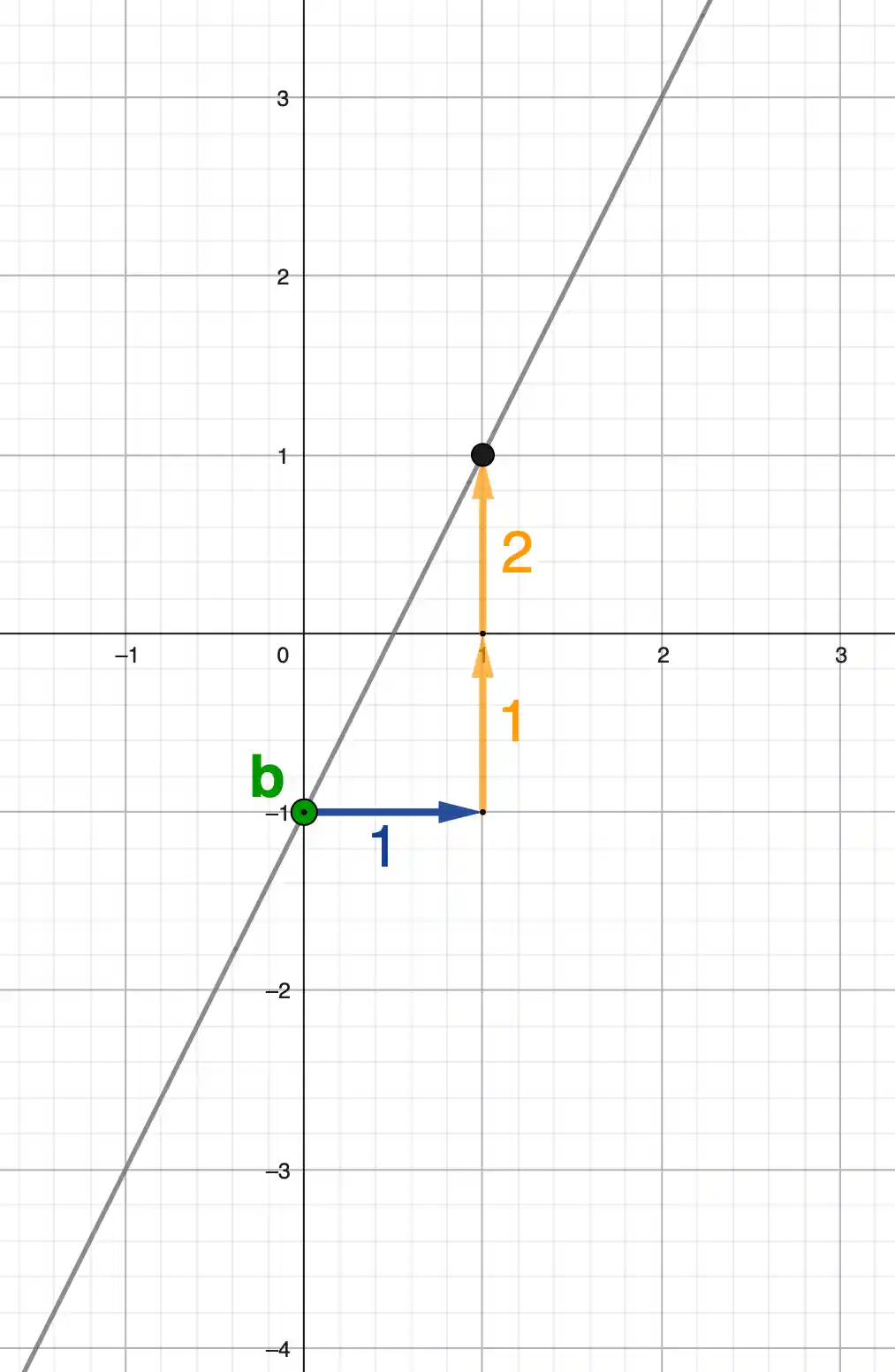
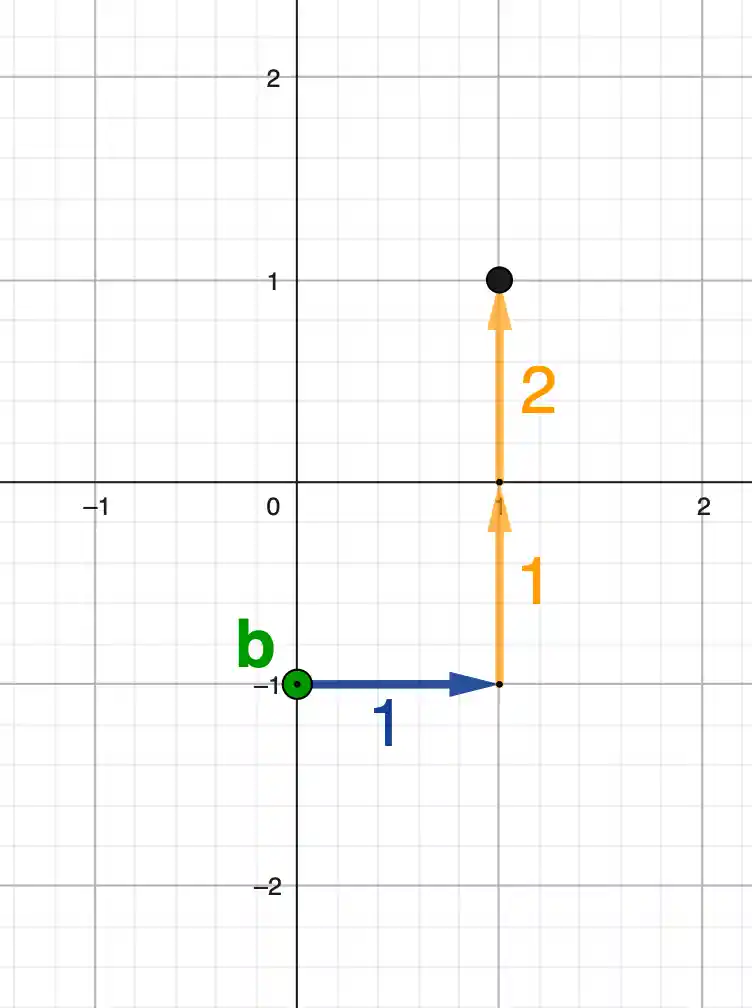
Geraden zeichnen
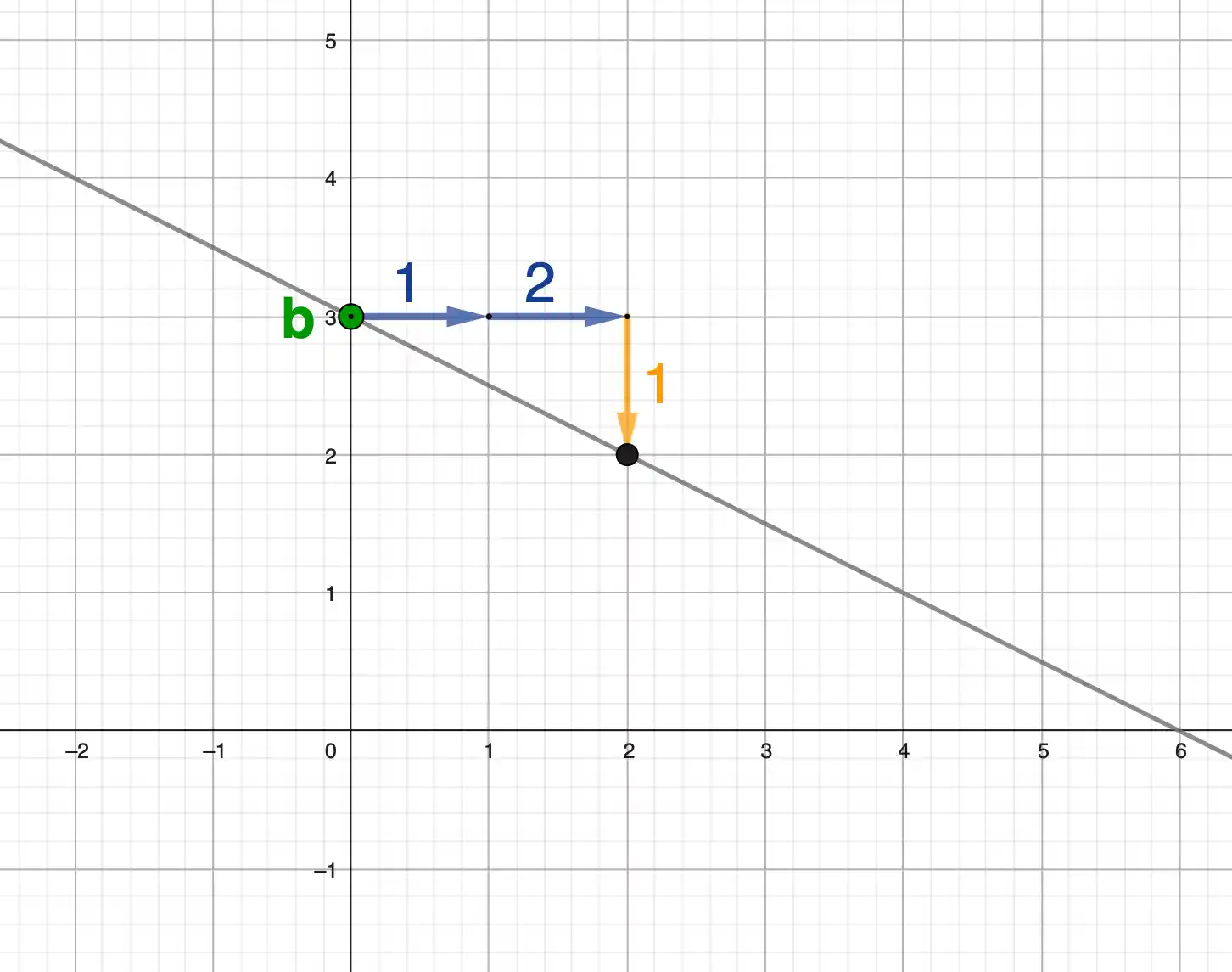
Lineare Funktionen zeichnest du immer gleich: Startpunkt mit \( {\textcolor{green}{b}} \) setzen, dann den Laufweg aus \( {\textcolor{orangered}{m}} \) gehen. Wir machen das direkt an zwei Beispielen.
\( f(x) = {\textcolor{orangered}{2}}x - {\textcolor{green}{1}} \)
\( f(x) = {\textcolor{orangered}{2}}x - {\textcolor{green}{1}} \)
1. Schritt:
Startpunkt →
y-Achsenabschnitt \( = {\textcolor{green}{b}} \).
\( {\textcolor{green}{b}} = {\textcolor{green}{-1}} \)
\( S_y = (0 \mid {\textcolor{green}{-1}}) \)
2. Schritt:
Steigung als Bruch schreiben.
\( {\textcolor{orangered}{m}} = {\textcolor{orangered}{2}}
= \dfrac{{\textcolor{orange}{2}}}{{\textcolor{midnightblue}{1}}} \)
3. Schritt:
Nenner nach rechts,
Zähler nach oben (weil \(m>0\)).
1 nach rechts ⟶
2 nach oben ↑
4. Schritt:
Zweiten Punkt setzen → verbinden → Gerade fertig.
Und jetzt genau das Gleiche mit negativer Steigung: Der Laufweg geht dann nach unten.
\( f(x)= {\textcolor{orangered}{-\dfrac{1}{2}}}x + {\textcolor{green}{3}} \)
\( f(x)= {\textcolor{orangered}{-\dfrac{1}{2}}}x + {\textcolor{green}{3}} \)
1. Schritt:
\( {\textcolor{green}{b}} = {\textcolor{green}{3}} \)
→ Startpunkt \( (0 \mid {\textcolor{green}{3}}) \)
2. Schritt:
\( {\textcolor{orangered}{m}} = -\dfrac{{\textcolor{orange}{1}}}{{\textcolor{midnightblue}{2}}} \)
3. Schritt:
2 nach rechts,
1 nach unten (weil \(m < 0\)).
2 nach rechts ⟶
1 nach unten ↓
4. Schritt:
Zweiten Punkt setzen → verbinden → Gerade fertig.
Wichtig
\( f(x)= {\textcolor{orangered}{m}}x + {\textcolor{green}{b}} \)
• \( {\textcolor{green}{b}} \) ist der Startpunkt auf der y-Achse: \( (0 \mid b) \)
• \( {\textcolor{orangered}{m}} \) ist der Laufweg zum zweiten Punkt (als Bruch!)
• Nenner → nach rechts
• Zähler → nach oben ( \(m>0\) ) oder nach unten ( \(m < 0\) )
Merke
Zum Zeichnen brauchst du nur zwei Punkte:
• \( (0 \mid b) \) setzen
• \( m \) als Bruch lesen: rechts (Nenner),
dann hoch/runter (Zähler)
\( {\textcolor{orangered}{m}} =
\dfrac{{\textcolor{orange}{Zähler}}}{{\textcolor{midnightblue}{Nenner}}} \)
Gleichung aufstellen
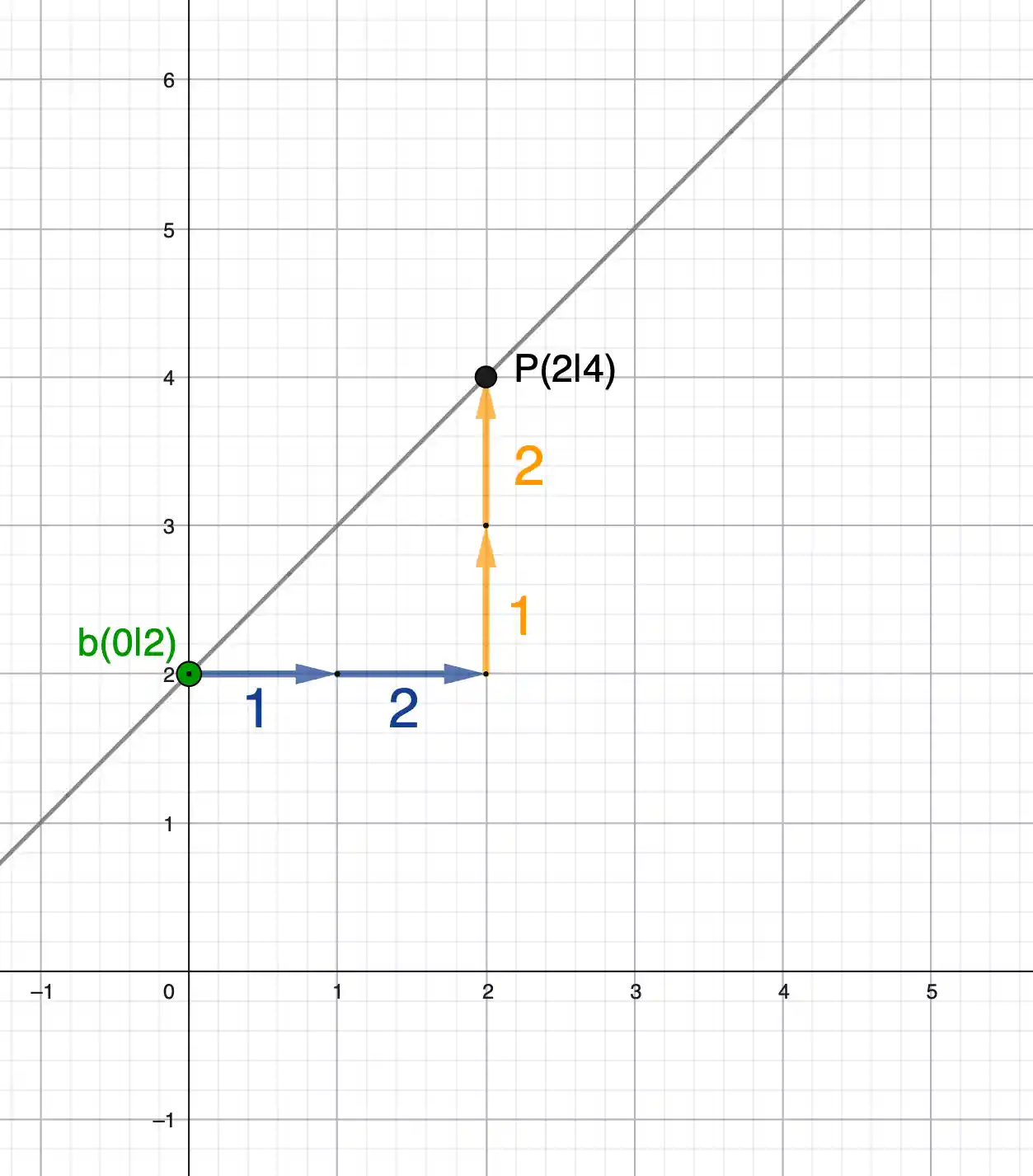
Jetzt drehen wir das Ganze um: Wir lesen die Funktionsgleichung aus der Zeichnung ab.
1. Schritt: \( {\textcolor{green}{b}} \) am Schnittpunkt mit der y-Achse ablesen.
\( (0 \mid {\textcolor{green}{2}}) \)
\( {\textcolor{green}{b}} = {\textcolor{green}{2}} \)
2. Schritt: Einen weiteren gut ablesbaren Punkt wählen.
\( P(2 \mid 4) \)
3. Schritt: Den Laufweg von \( {\textcolor{green}{b}} \) nach \( P \) eintragen.
\( {\color{blue}{2}} \quad \) nach rechts
\( {\color{orange}{2}} \quad \) nach oben
4. Schritt: Laufweg als Bruch schreiben
→ Zähler = hoch/runter, Nenner = rechts.
\( {\textcolor{orangered}{m}} =
\dfrac{{\color{orange}{2}}}{{\color{blue}{2}}}
= {\textcolor{orangered}{1}} \)
5. Schritt: \( {\textcolor{orangered}{m}} \) und \( {\textcolor{green}{b}} \) in die Grundform einsetzen.
\( f(x) = {\textcolor{orangered}{m}}x + {\textcolor{green}{b}} \)
\( f(x) = {\textcolor{orangered}{1}}x + {\textcolor{green}{2}} \)
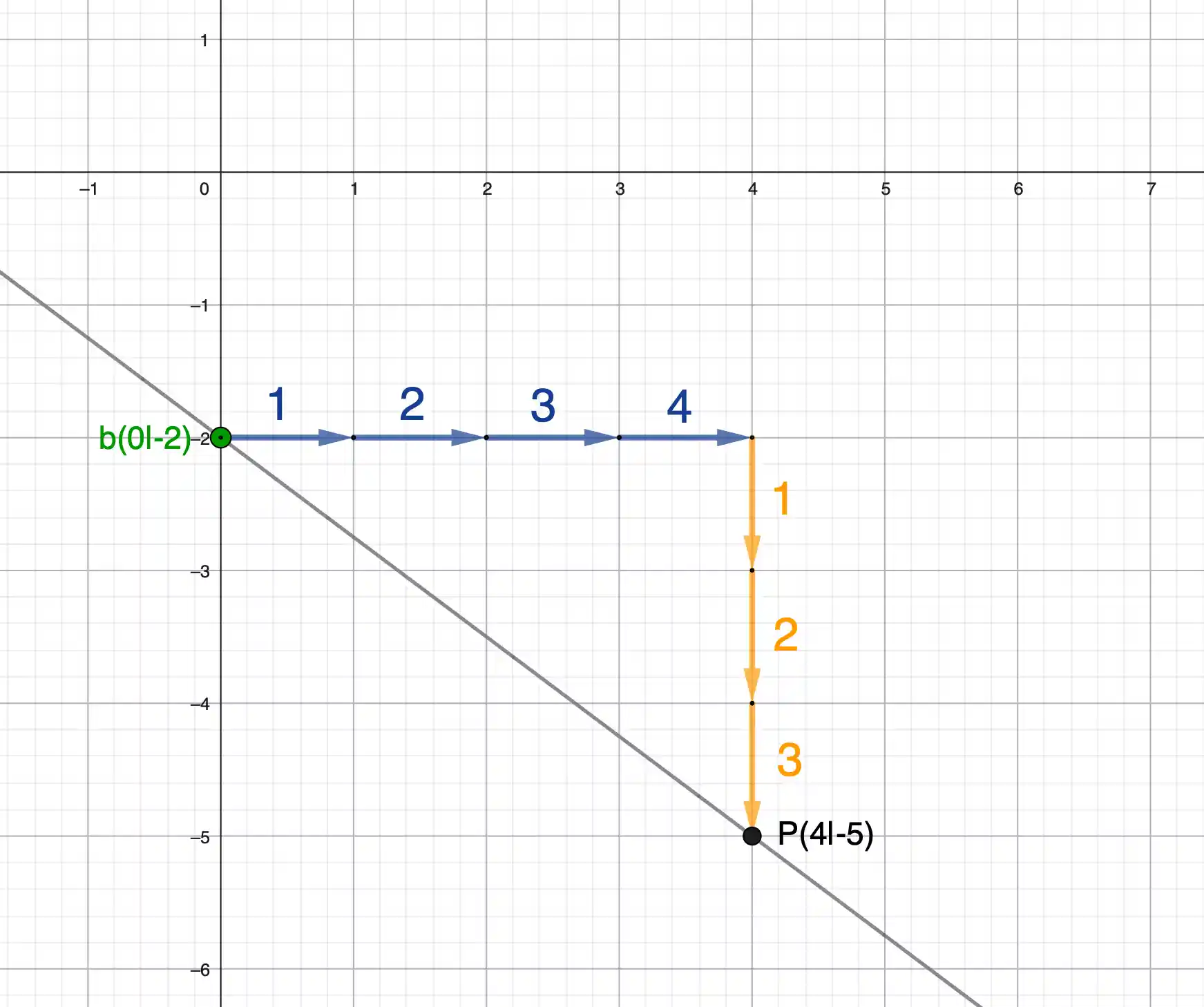
Jetzt das Gleiche nochmal – aber mit negativer Steigung.
1. Schritt: \( {\textcolor{green}{b}} \) am Schnittpunkt mit der y-Achse ablesen.
\( (0 \mid {\textcolor{green}{-2}}) \)
\( {\textcolor{green}{b}} = {\textcolor{green}{-2}} \)
2. Schritt: Einen weiteren gut ablesbaren Punkt wählen.
\( P(4 \mid -5) \)
3. Schritt: Den Laufweg von \( {\textcolor{green}{b}} \) nach \( P \) eintragen.
\( {\color{blue}{4}} \quad \) nach rechts
\( {\color{orange}{3}} \quad \) nach unten
4. Schritt: Laufweg als Bruch schreiben
→ Zähler = hoch/runter, Nenner = rechts.
\( {\textcolor{orangered}{m}} =
-\dfrac{{\color{orange}{3}}}{{\color{blue}{4}}}
= {\textcolor{orangered}{-\dfrac{3}{4}}} \)
Laufweg nach unten –
Steigung negativ.
5. Schritt: \( {\textcolor{orangered}{m}} \) und \( {\textcolor{green}{b}} \) in die Grundform einsetzen.
\( f(x) = {\textcolor{orangered}{m}}x + {\textcolor{green}{b}} \)
\( f(x) = {\textcolor{orangered}{-\dfrac{3}{4}}}x + {\textcolor{green}{-2}} \)
Merke
\( f(x)= {\textcolor{orangered}{m}}x + {\textcolor{green}{b}} \)
- \( {\textcolor{green}{b}} \) liest du am Schnittpunkt mit der y-Achse ab: \( (0 \mid {\textcolor{green}{b}}) \)
-
Die Steigung ergibt sich aus dem
Laufweg:
\( {\textcolor{orangered}{m}} = \dfrac{{\color{orange}{\text{hoch / runter}}}}{{\color{blue}{\text{rechts}}}} \)
- Laufweg nach oben → Steigung positiv
- Laufweg nach unten → Steigung negativ
Gleichung aufstellen: Steigungsformel
Du suchst Profi-Nachhilfe mit echtem Impact? Dann bist du bei OnMathe genau richtig!
Mehr dazu
Weiterführende Informationen
Die Tangente - eine lineare Funktion
lineare Funktionen im LGS
Treffen sich zwei lineare Funktionen, entsteht ein Schnittpunkt. Dieser Punkt ist die Lösung des linearen Gleichungssystems.
\( \textsf{I:}\; {\textcolor{orange}{y}} = 2\cdot{\textcolor{blue}{x}} + 1 \)
\( \textsf{II:}\; {\textcolor{orange}{y}} = -{\textcolor{blue}{x}} + 4 \)
Grafisch: Schnittpunkt im Koordinatensystem ablesen.
\( S({\textcolor{blue}{1}} \mid {\textcolor{orange}{3}}) \)
Rechnerisch: Funktionen gleichsetzen und lösen.
\( 2{\textcolor{blue}{x}} + 1 = -{\textcolor{blue}{x}} + 4 \hspace{1cm} |{\textcolor{orangered}{+}}{\textcolor{blue}{x}} \)
\( 3{\textcolor{blue}{x}} + 1 = 4 \hspace{1cm} |{\textcolor{orangered}{-}}1 \)
\( 3{\textcolor{blue}{x}} = 3 \hspace{1cm} |:3 \)
\( {\textcolor{blue}{x}} = {\textcolor{blue}{1}} \)
\( {\textcolor{blue}{x}} = {\textcolor{blue}{1}} \) in eine Gleichung einsetzen.
\( {\textcolor{orange}{y}} = 2{\textcolor{blue}{x}} + 1 \)
\( {\textcolor{orange}{y}} = 2\cdot{\textcolor{blue}{1}} + 1 \)
\( {\textcolor{orange}{y}} = {\textcolor{orange}{3}} \)
\( S({\textcolor{blue}{1}} \mid {\textcolor{orange}{3}}) \)
→ Grafisch und rechnerisch kommt derselbe Schnittpunkt raus.
Wichtig
Der Schnittpunkt liegt auf beiden Geraden –
er ist also Lösung beider Geraden.
Merke
• Schnittpunkt = Lösung des LGS
• Grafisch: ablesen | Rechnerisch: gleichsetzen
Parallele und senkrechte Geraden
Punktprobe
Wusstest du schon... ?
