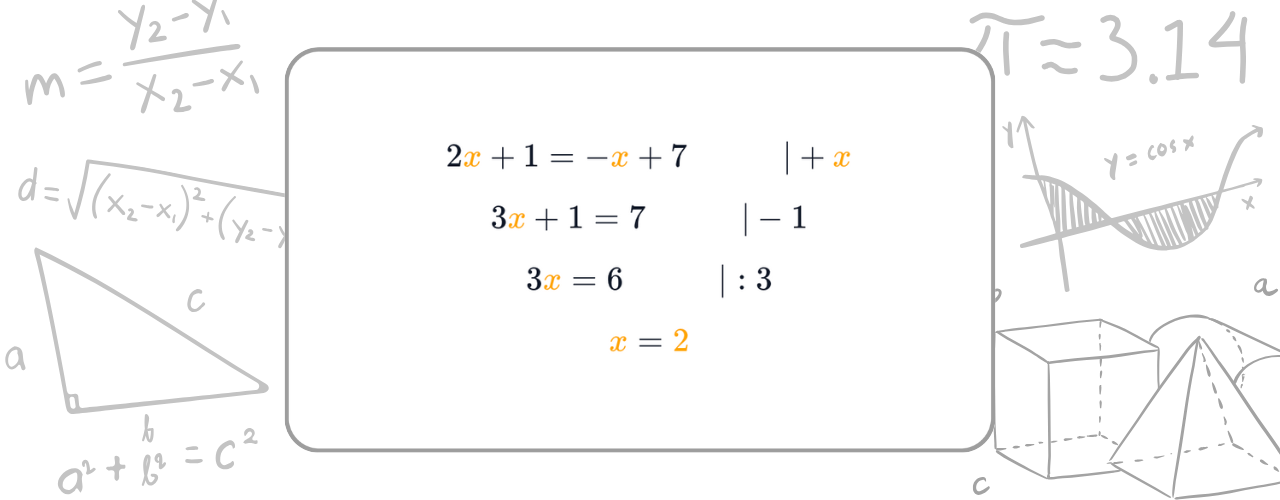lineare Gleichungssysteme

Einsetzungsverfahren

Lisa von OnMathe
two students high five

Einleitung

Mit dem Einsetzungsverfahren löst du ein lineares Gleichungssystem, indem du eine Gleichung nach einer Variable auflöst und diesen Ausdruck in die andere Gleichung einsetzt.

Wir starten sofort mit einem Beispiel:
\( \textsf{I. } \ \ {\textcolor{orange}{x}} = 6 - 2{\textcolor{green}{y}} \)
\( \textsf{II. } \ \ 3{\textcolor{orange}{x}} + 2{\textcolor{green}{y}} = 10 \)
1. Schritt: Ausdruck aus Gleichung I in Gleichung II einsetzen.
\( 3{\textcolor{orange}{x}} + 2{\textcolor{green}{y}} = 10 \)
\( 3({\textcolor{orange}{6 - 2y}}) + 2{\textcolor{green}{y}} = 10 \)
2. Schritt: Nach \( {\textcolor{green}{y}} \) auflösen.
\( 18 - 6{\textcolor{green}{y}} + 2{\textcolor{green}{y}} = 10 \)
\( 18 - 4{\textcolor{green}{y}} = 10 \hspace{1cm} |-18 \)
\( -4{\textcolor{green}{y}} = -8 \hspace{1cm} |:(-4) \)
\( {\textcolor{green}{y}} = {\textcolor{green}{2}} \)
3. Schritt: \( {\textcolor{green}{y=2}} \) in Gleichung I einsetzen.
\( {\textcolor{orange}{x}} = 6 - 2\cdot{\textcolor{green}{2}} \)
\( {\textcolor{orange}{x}} = {\textcolor{orange}{2}} \)
4. Schritt: Lösung als Punkt notieren.
\( \textsf{L}\big({\textcolor{orange}{2}} \mid {\textcolor{green}{2}}\big) \)

Eine Gleichung umstellen, einsetzen und losrechnen.
Wie das genau funktioniert, übst du im Beitrag Schritt für Schritt mit Aufgaben.

Merke
1. Eine Gleichung nach einer Variable auflösen
2. Ausdruck in die andere Gleichung einsetzen
3. Erste Variable berechnen → rückeinsetzen

Inhaltsverzeichnis

Das erwartet Dich

Einleitung
Beispiel 1: Schritt für Schritt
Beispiel 2: Gleichungen umstellen
Textaufgaben lösen

Einleitung

Mit dem Einsetzungsverfahren löst du ein lineares Gleichungssystem, indem du eine Gleichung nach einer Variable auflöst und diesen Ausdruck in die andere Gleichung einsetzt.

Wir starten sofort mit einem Beispiel:
\( \textsf{I. } \ \ {\textcolor{orange}{x}} = 6 - 2{\textcolor{green}{y}} \)
\( \textsf{II. } \ \ 3{\textcolor{orange}{x}} + 2{\textcolor{green}{y}} = 10 \)
1. Schritt: Ausdruck aus Gleichung I in Gleichung II einsetzen.
\( 3{\textcolor{orange}{x}} + 2{\textcolor{green}{y}} = 10 \)
\( 3({\textcolor{orange}{6 - 2y}}) + 2{\textcolor{green}{y}} = 10 \)
2. Schritt: Nach \( {\textcolor{green}{y}} \) auflösen.
\( 18 - 6{\textcolor{green}{y}} + 2{\textcolor{green}{y}} = 10 \)
\( 18 - 4{\textcolor{green}{y}} = 10 \hspace{1cm} |-18 \)
\( -4{\textcolor{green}{y}} = -8 \hspace{1cm} |:(-4) \)
\( {\textcolor{green}{y}} = {\textcolor{green}{2}} \)
3. Schritt: \( {\textcolor{green}{y=2}} \) in Gleichung I einsetzen.
\( {\textcolor{orange}{x}} = 6 - 2\cdot{\textcolor{green}{2}} \)
\( {\textcolor{orange}{x}} = {\textcolor{orange}{2}} \)
4. Schritt: Lösung als Punkt notieren.
\( \textsf{L}\big({\textcolor{orange}{2}} \mid {\textcolor{green}{2}}\big) \)

Eine Gleichung umstellen, einsetzen und losrechnen.
Wie das genau funktioniert, übst du im Beitrag Schritt für Schritt mit Aufgaben.

Merke
1. Eine Gleichung nach einer Variable auflösen
2. Ausdruck in die andere Gleichung einsetzen
3. Erste Variable berechnen → rückeinsetzen

Beispiel 1: Schritt für Schritt

Wir lösen ein lineares Gleichungssystem mit dem Einsetzungsverfahren.
Ziel: Eine Gleichung wird nach einer Variable umgestellt und in die andere eingesetzt.

\( \textsf{I. } \ \ {\textcolor{orange}{x}} = 4 - {\textcolor{green}{y}} \)
\( \textsf{II. } \ \ 2{\textcolor{orange}{x}} + {\textcolor{green}{y}} = 7 \)

Gleichung I ist bereits nach \(x\) aufgelöst. Diesen Ausdruck können wir direkt in Gleichung II einsetzen.

1. Schritt: Ausdruck aus Gleichung I in Gleichung II einsetzen.
\( 2{\textcolor{orange}{x}} + {\textcolor{green}{y}} = 7 \)
\( 2({\textcolor{orange}{4 - y}}) + {\textcolor{green}{y}} = 7 \)

Jetzt kommt nur noch eine Variable vor – wir können ganz normal weiterrechnen.

\( 8 - 2{\textcolor{green}{y}} + {\textcolor{green}{y}} = 7 \)
\( 8 - {\textcolor{green}{y}} = 7 \hspace{1cm} |-8 \)
\( -{\textcolor{green}{y}} = -1 \hspace{1cm} |\cdot(-1) \)
\( {\textcolor{green}{y}} = {\textcolor{green}{1}} \)
2. Schritt: \( {\textcolor{green}{y}} \) in Gleichung I einsetzen.
\( {\textcolor{orange}{x}} = 4 - {\textcolor{green}{y}} \)
\( {\textcolor{orange}{x}} = 4 - {\textcolor{green}{1}} \)
\( {\textcolor{orange}{x}} = {\textcolor{orange}{3}} \)
3. Schritt: Lösung als Punkt notieren.
\( \textsf{L}\big({\textcolor{orange}{3}} \mid {\textcolor{green}{1}}\big) \)

Ergebnis: Die beiden Geraden schneiden sich in \( \big({\textcolor{orange}{3}} \mid {\textcolor{green}{1}}\big) \).

Wichtig
Du kannst selbst entscheiden, welche Variable du zuerst umstellst.
Praktisch ist die Gleichung, die sich leicht umformen lässt.
Merke
1) Eine Gleichung nach einer Variable umstellen
2) Ausdruck in die andere Gleichung einsetzen
3) Eine Variable berechnen
4) Rückeinsetzen → zweite Variable → Punkt \( \big(x \mid y\big) \)

Beispiel 2: Gleichungen umstellen

Nicht immer steht eine Gleichung schon so da, dass man sofort einsetzen kann. Oft müssen wir sie zuerst so vorbereiten, dass eine Variable allein steht.

Schauen wir uns das direkt an einem Beispiel an.

\( \textsf{I. } \ \ 2{\textcolor{orange}{x}} + {\textcolor{green}{y}} = {\textcolor{midnightblue}{8}} \)
\( \textsf{II. } \ \ {\textcolor{orange}{x}} - {\textcolor{green}{y}} = {\textcolor{midnightblue}{1}} \)

So wie die Gleichungen hier stehen, können wir noch nichts direkt einsetzen. Also stellen wir zuerst eine Gleichung nach einer Variable um.

Wir stellen Gleichung II nach \( {\textcolor{orange}{x}} \) um.
\( {\textcolor{orange}{x}} - {\textcolor{green}{y}} = {\textcolor{midnightblue}{1}} \hspace{1cm} |+{\textcolor{green}{y}} \)
\( {\textcolor{orange}{x}} = {\textcolor{midnightblue}{1}} + {\textcolor{green}{y}} \)
Merke
Ziel ist immer: Eine Variable steht allein, damit du sie einsetzen kannst.

Als erstes setzen wir den Ausdruck für \( {\textcolor{orange}{x}} \) in Gleichung I ein.

\( 2{\textcolor{orange}{x}} + {\textcolor{green}{y}} = {\textcolor{midnightblue}{8}} \)
\( 2({\textcolor{orange}{1 + y}}) + {\textcolor{green}{y}} = {\textcolor{midnightblue}{8}} \)

Jetzt kommt nur noch \( {\textcolor{green}{y}} \) vor – wir rechnen weiter.

\( 2 + 2{\textcolor{green}{y}} + {\textcolor{green}{y}} = 8 \)
\( 2 + 3{\textcolor{green}{y}} = 8 \hspace{1cm} |-2 \)
\( 3{\textcolor{green}{y}} = 6 \hspace{1cm} |:3 \)
\( {\textcolor{green}{y}} = {\textcolor{green}{2}} \)
Zum Schluss setzen wir \( {\textcolor{green}{y}} \) wieder in Gleichung II ein.
\( {\textcolor{orange}{x}} = 1 + {\textcolor{green}{y}} \)
\( {\textcolor{orange}{x}} = 1 + {\textcolor{green}{2}} \)
\( {\textcolor{orange}{x}} = {\textcolor{orange}{3}} \)

Damit kennen wir beide Variablen.

\( {\textcolor{orange}{x}} = {\textcolor{orange}{3}} \)
\( {\textcolor{green}{y}} = {\textcolor{green}{2}} \)
Zum Schluss schreiben wir die Lösung als Punkt.
\( \textsf{L}\big({\textcolor{orange}{3}} \mid {\textcolor{green}{2}}\big) \)
Merke
• Vor dem Einsetzen immer erst eine Gleichung umstellen.
• Den eingesetzten Ausdruck immer in Klammern schreiben.
• Die Lösung am Ende als Punkt notieren: \((x \mid y)\).

Textaufgaben lösen

In Anwendungsaufgaben geht es nicht nur ums Rechnen. Zuerst musst du einen Text verstehen und daraus passende Gleichungen aufstellen. Genau das schauen wir uns jetzt Schritt für Schritt an.

Beispiel
Zwei Kinokarten kosten zusammen 18 €.
Die Erwachsenenkarte kostet 4 € mehr als die Kinderkarte.
Wie teuer ist jede Karte?

Zuerst sammeln wir die wichtigen Informationen aus dem Text.

Gesamtkosten: 18 €
Erwachsene: 4 € mehr
Kinderkarte: günstiger

Jetzt legen wir fest, wofür unsere Variablen stehen.

\( {\textcolor{green}{y}} = \) Preis der Kinderkarte
\( {\textcolor{orange}{x}} = \) Preis der Erwachsenenkarte

Aus dem Text formulieren wir nun die Gleichungen. Zunächst in Worten und dann setzen wir unsere Variablen ein.

\( \textsf{I. } \ \textsf{Preis Erw.} = \textsf{Preis Kinder} + 4 \)
\( \textsf{II. } \ \textsf{Preis Erw.} + \textsf{Preis Kinder} = 18 \)
\( \textsf{I. } \ {\textcolor{orange}{x}} = {\textcolor{green}{y}} + 4 \)
\( \textsf{II. } \ {\textcolor{orange}{x}} + {\textcolor{green}{y}} = 18 \)

Für das Einsetzungsverfahren ist das ideal: Gleichung I ist bereits nach \( {\textcolor{orange}{x}} \) aufgelöst.

Wir setzen den Ausdruck aus Gleichung I in Gleichung II ein.

\( {\textcolor{orange}{x}} + {\textcolor{green}{y}} = 18 \)
\( ({\textcolor{orange}{y + 4}}) + {\textcolor{green}{y}} = 18 \)

Jetzt kommt nur noch eine Variable vor – wir rechnen weiter.

\( 2{\textcolor{green}{y}} + 4 = 18 \hspace{1cm} |-4 \)
\( 2{\textcolor{green}{y}} = 14 \hspace{1cm} |:2 \)
\( {\textcolor{green}{y}} = 7 \)

Am Ende setzen wir \( {\textcolor{green}{y}} = 7 \) in Gleichung I ein.

\( {\textcolor{orange}{x}} = {\textcolor{green}{y}} + 4 \)
\( {\textcolor{orange}{x}} = 7 + 4 \)
\( {\textcolor{orange}{x}} = 11 \)

Damit kennen wir beide Preise.

Die Kinderkarte kostet \( {\textcolor{green}{7}} \) € und die Erwachsenenkarte \( {\textcolor{orange}{11}} \) €.
Merke
• Text lesen → Abhängigkeiten erkennen
• Eine Gleichung beschreibt oft direkt: „… ist … mehr als …“
• Diese Gleichung einsetzen und weiterrechnen
• Ergebnis als Antwort formulieren

Du suchst Profi-Nachhilfe mit echtem Impact? Dann bist du bei OnMathe genau richtig!

Verstehe Mathe ab der ersten Stunde.

Mathe Nachhilfe online
Student lernt draußen im freien mit Notebook

Teste dein Wissen

Übungen

Löse mit dem Einsetzungsverfahren

\( \textsf{I. } \ \ 2{\textcolor{orange}{x}} + {\textcolor{green}{y}} = 6 \)
\( \textsf{II. } \ \ 3{\textcolor{orange}{x}} - {\textcolor{green}{y}} = 9 \)

Lösung

Schritt 1: Stelle Gleichung I nach \( {\textcolor{green}{y}} \) um.

\( {\textcolor{green}{y}} = 6 - 2{\textcolor{orange}{x}} \)

Schritt 2: Setze den Ausdruck in Gleichung II ein.

\( 3{\textcolor{orange}{x}} - (6 - 2{\textcolor{orange}{x}}) = 9 \)
\( 5{\textcolor{orange}{x}} = 15 \hspace{1cm} |:5 \)
\( {\textcolor{orange}{x}} = 3 \)

Schritt 3: Rückeinsetzen.

\( {\textcolor{green}{y}} = 6 - 2\cdot 3 = 0 \)
Lösung: \( \textsf{L}(3 \mid 0) \)

\( \textsf{I. } \ \ 2{\textcolor{orange}{x}} + {\textcolor{green}{y}} = 7 \)
\( \textsf{II. } \ \ 3{\textcolor{orange}{x}} - 2{\textcolor{green}{y}} = 4 \)

Lösung

Schritt 1: Stelle Gleichung I nach \( {\textcolor{green}{y}} \) um.

\( {\textcolor{green}{y}} = 7 - 2{\textcolor{orange}{x}} \)

Schritt 2: Setze in Gleichung II ein.

\( 3{\textcolor{orange}{x}} - 2(7 - 2{\textcolor{orange}{x}}) = 4 \)
\( 7{\textcolor{orange}{x}} = 18 \hspace{1cm} |:7 \)
\( {\textcolor{orange}{x}} = {\textcolor{orange}{\dfrac{18}{7}}} \)

Schritt 3: Rückeinsetzen.

\( {\textcolor{green}{y}} = 7 - 2\cdot\dfrac{18}{7} = \dfrac{13}{7} \)
Lösung: \( \textsf{L}\!\big(\tfrac{18}{7} \mid \tfrac{13}{7}\big) \)

Textaufgabe:
In einer Schule gibt es 26 Schüler im Fußballverein oder im Basketballverein.
Ein Fußballer zahlt 2 €, ein Basketballer 4 €.
Insgesamt werden 88 € an Beiträgen gezahlt.

Lösung

Schritt 1: Lege die Variablen fest.

\( {\textcolor{orange}{x}} = \) Anzahl Fußballer
\( {\textcolor{green}{y}} = \) Anzahl Basketballer

Schritt 2: Stelle die Gleichungen auf.

\( \textsf{I. } \ {\textcolor{orange}{x}} + {\textcolor{green}{y}} = 26 \)
\( \textsf{II. } \ 2{\textcolor{orange}{x}} + 4{\textcolor{green}{y}} = 88 \)

Schritt 3: Stelle Gleichung I nach \( {\textcolor{orange}{x}} \) um.

\( {\textcolor{orange}{x}} = 26 - {\textcolor{green}{y}} \)

Schritt 4: Setze in Gleichung II ein.

\( 2(26 - {\textcolor{green}{y}}) + 4{\textcolor{green}{y}} = 88 \)
\( 52 + 2{\textcolor{green}{y}} = 88 \hspace{1cm} |-52 \)
\( {\textcolor{green}{y}} = 18 \)

Schritt 5: Rückeinsetzen.

\( {\textcolor{orange}{x}} = 26 - 18 = 8 \)

Antwort:

Es gibt \( {\textcolor{orange}{8}} \) Fußballer und \( {\textcolor{green}{18}} \) Basketballer.

Ausgewählt für Dich

Empfohlene Beiträge

Gleichsetzungsverfahren einfach erklärt: Lineare Gleichungssysteme Schritt für Schritt lösen – auch bei Textaufgaben

Gleichsetzungsverfahren

Gleichsetzungsverfahren einfach erklärt: Lineare Gleichungssysteme Schritt für Schritt lösen – auch bei Textaufgaben

Additionsverfahren einfach erklärt: Lineare Gleichungssysteme Schritt für Schritt lösen – auch bei Textaufgaben

Additionsverfahren

Additionsverfahren einfach erklärt: Lineare Gleichungssysteme Schritt für Schritt lösen – auch bei Textaufgaben

Lineares Gleichungssystem zeichnerisch lösen: So erkennst du eine, keine oder unendlich viele Lösungen im Koordinatensystem

lineare Gleichungssysteme zeichnerisch lösen

Lineares Gleichungssystem zeichnerisch lösen: So erkennst du eine, keine oder unendlich viele Lösungen im Koordinatensystem

Mehr dazu

in unseren FAQs

Wann ist das Einsetzungsverfahren sinnvoll?

Das Einsetzungsverfahren ist besonders sinnvoll, wenn eine Gleichung bereits nach einer Variable aufgelöst ist oder sich leicht auflösen lässt.
Typisch ist:
→ eine Variable steht schon allein
→ z. B. \( y = 2x + 1 \)

Welche Gleichung löse ich zuerst auf?

Immer die einfachere Gleichung.
→ möglichst wenige Terme
→ am besten ohne Brüche
So vermeidest du unnötige Rechenfehler.

Was passiert nach dem Einsetzen?

Nach dem Einsetzen erhältst du eine Gleichung mit nur einer Variablen.
Diese löst du ganz normal.
Anschließend setzt du den Wert wieder in die andere Gleichung ein.

Welche Fehler passieren beim Einsetzungsverfahren häufig?

Typische Fehler sind:
→ Klammern beim Einsetzen vergessen
→ falsch nach einer Variable aufgelöst
→ der zweite Wert wird nicht berechnet

Muss ich immer das Einsetzungsverfahren verwenden?

Nein.
Es gibt mehrere Lösungsverfahren.
→ Nutze immer das Verfahren,
→ das am übersichtlichsten ist.

Mehr dazu

Weiterführende Informationen

Einsetzungsverfahren: Erst vorbereiten, dann einsetzen

Beim Einsetzungsverfahren bereitest du die Gleichungen oft zuerst vor, z. B. durch Multiplizieren, damit du anschließend sauber umstellen und einsetzen kannst.

\( \textsf{I.}\quad 2{\textcolor{orange}{x}} + 3{\textcolor{green}{y}} = {\textcolor{midnightblue}{22}} \)
\( \textsf{II.}\quad 0{,}5{\textcolor{orange}{x}} + 2{\textcolor{green}{y}} = {\textcolor{midnightblue}{8}} \)
Ansage: Zuerst bringen wir eine Gleichung in die Form \( {\textcolor{orange}{x}} = \dots \) oder \( {\textcolor{green}{y}} = \dots \). Welche Variable du wählst, bleibt dir überlassen..
1. Schritt: Gleichung II mit 2 multiplizieren (0,5 verschwindet).
\[ \begin{array}{rcrccr} 0{,}5{\textcolor{orange}{x}} & + & 2{\textcolor{green}{y}} & = & {\textcolor{midnightblue}{8}} \\ \big|\,{\textcolor{orangered}{\cdot 2}} & & \big|\,{\textcolor{orangered}{\cdot 2}} & & \big|\,{\textcolor{orangered}{\cdot 2}} \\ {\textcolor{orange}{x}} & + & 4{\textcolor{green}{y}} & = & {\textcolor{midnightblue}{16}} \end{array} \]
2. Schritt: Neue Gleichung II nach \({\textcolor{orange}{x}}\) auflösen.
\( {\textcolor{orange}{x}} + 4{\textcolor{green}{y}} = {\textcolor{midnightblue}{16}} \hspace{1cm} |{\textcolor{orangered}{-}}4{\textcolor{green}{y}} \)
\( {\textcolor{orange}{x}} = {\textcolor{orange}{16 - 4{\textcolor{green}{y}}}} \)
3. Schritt: In Gleichung I einsetzen und \( {\textcolor{green}{y}} \) berechnen.
\( 2\cdot {\textcolor{orange}{\big(16 - 4{\textcolor{green}{y}}\big)}} + 3{\textcolor{green}{y}} = {\textcolor{midnightblue}{22}} \)
\( 32 - 8{\textcolor{green}{y}} + 3{\textcolor{green}{y}} = {\textcolor{midnightblue}{22}} \)
\( 32 - 5{\textcolor{green}{y}} = {\textcolor{midnightblue}{22}} \hspace{1cm} |{\textcolor{orangered}{-}}32 \)
\( -5{\textcolor{green}{y}} = {\textcolor{midnightblue}{-10}} \hspace{1cm} |:({\textcolor{orangered}{-5}}) \)
\( {\textcolor{green}{y}} = {\textcolor{green}{2}} \)
4. Schritt: \( {\textcolor{green}{y}} \) einsetzen und \( {\textcolor{orange}{x}} \) berechnen.
\( {\textcolor{orange}{x}} = {\textcolor{midnightblue}{16}} - 4\cdot{\textcolor{green}{2}} \)
\( {\textcolor{orange}{x}} = {\textcolor{orange}{8}} \)
Ergebnis: Lösung als Punkt notieren.
\( \textsf{L}\big({\textcolor{orange}{8}} \mid {\textcolor{green}{2}}\big) \)
Merke
Prüfungsfall (typisch): Dezimalzahl wie \(0{,}5\) ist drin.
1) multiplizieren, bis keine Dezimalzahl mehr da ist
2) nach einer Variable umstellen (am einfachsten wählen)
3) einsetzen → eine Variable bleibt übrig
4) lösen und zurück einsetzen

Das richtige Verfahren erkennen

Wichtig ist nicht nur das Rechnen, sondern das passende Verfahren. Hier siehst du kurz und klar, wann welches Verfahren passt.

\( \textsf{I.}\quad {\textcolor{green}{y}} = 2{\textcolor{orange}{x}} - 3 \)
\( \textsf{II.}\quad {\textcolor{orange}{x}} + 3{\textcolor{green}{y}} = 9 \)
→ \(y\) ist bereits freigestellt
→ Einsetzen geht sofort
→ Einsetzungsverfahren

Das Einsetzungsverfahren ist besonders dann sinnvoll, wenn eine Variable schon allein steht oder sich mit wenigen Umformungen freistellen lässt.

→ Ausdruck einsetzen
→ eine Gleichung mit nur einer Variablen lösen
\( \textsf{I.}\quad 4{\textcolor{orange}{x}} + 2{\textcolor{green}{y}} = 14 \)
\( \textsf{II.}\quad -4{\textcolor{orange}{x}} - 5{\textcolor{green}{y}} = 1 \)
→ \(x\) ist in beiden Gleichungen gleich
→ beim addieren fällt \(x\) direkt weg
→ Additionsverfahren
Du willst sehen, wie man hier sauber rechnet? Dann schau dir unseren Beitrag Additionsverfahren an.
\( \textsf{I.}\quad {\textcolor{green}{y}} = -{\textcolor{orange}{x}} + 6 \)
\( \textsf{II.}\quad {\textcolor{green}{y}} = 0{,}5{\textcolor{orange}{x}} + 3 \)
→ beide Gleichungen sind nach \(y\) aufgelöst
→ du kannst direkt gleichsetzen
→ Gleichsetzungsverfahren
Du willst wissen, wie das Gleichsetzen funktioniert? Dann schau dir unseren Beitrag Gleichsetzungsverfahren an.
Merke
Es gibt nicht das eine beste Verfahren.
→ Schau dir die Gleichungen an
→ wähle das Verfahren, das am wenigsten Umformungen braucht

Typische Fehler beim Einsetzungsverfahren

Wer die typischen Fehler beim Einsetzungsverfahren kennt, kann sie vermeiden – erst falsch, dann richtig erklärt.

\( \textsf{I.}\quad {\textcolor{orange}{x}} = 2{\textcolor{green}{y}} - 1 \)
\( \textsf{II.}\quad 3{\textcolor{orange}{x}} + {\textcolor{green}{y}} = {\textcolor{midnightblue}{11}} \)
Typischer Fehler: Beim Einsetzen werden die Klammern vergessen.
\( 3\cdot {\textcolor{orangered}{2{\textcolor{green}{y}} - 1}} + {\textcolor{green}{y}} = 11 \)
Falsch gedacht: Das -1 gehört zum ganzen Ausdruck für \(x\).
Richtig: Der eingesetzte Ausdruck steht immer in Klammern.
\( 3\cdot(2{\textcolor{green}{y}} - 1) + {\textcolor{green}{y}} = {\textcolor{midnightblue}{11}} \)
\( \textsf{I.}\quad 5{\textcolor{orange}{x}} + {\textcolor{green}{y}} = {\textcolor{midnightblue}{9}} \)
\( \textsf{II.}\quad {\textcolor{orange}{x}} + 4{\textcolor{green}{y}} = {\textcolor{midnightblue}{8}} \)
Typischer Fehler: Es wird zu kompliziert nach einer Variable aufgelöst.
\( 5{\textcolor{orange}{x}} + {\textcolor{green}{y}} = {\textcolor{midnightblue}{9}} \hspace{1cm} |{\textcolor{orangered}{-}}{\textcolor{green}{y}} \)
\( 5{\textcolor{orange}{x}} = {\textcolor{midnightblue}{9}} - {\textcolor{green}{y}} \hspace{1cm} |:5 \)
\( {\textcolor{orange}{x}} = \dfrac{{\textcolor{midnightblue}{9}} - {\textcolor{green}{y}}}{5} \)
Problem: Es entstehen unnötige Brüche und das Einsetzen wird schnell unübersichtlich.
Richtig: Wähle eine Umformung, die möglichst einfach ist.
\( {\textcolor{orange}{x}} + 4{\textcolor{green}{y}} = {\textcolor{midnightblue}{8}} \hspace{1cm} |{\textcolor{orangered}{-}}4{\textcolor{green}{y}} \)
\( {\textcolor{orange}{x}} = {\textcolor{midnightblue}{8}} - 4{\textcolor{green}{y}} \)
\( \textsf{I.}\quad {\textcolor{orange}{x}} = 3{\textcolor{green}{y}} + 2 \)
\( \textsf{II.}\quad 2{\textcolor{orange}{x}} + {\textcolor{green}{y}} = {\textcolor{midnightblue}{14}} \)
Typischer Fehler: Es wird nur eine Variable berechnet.
\( {\textcolor{green}{y}} = {\textcolor{midnightblue}{2}} \)
Falsch: Die Lösung ist kein einzelner Wert.
Richtig: Beide Variablen gehören zur Lösung.
\( {\textcolor{orange}{x}} = 3\cdot{\textcolor{green}{2}} + 2 \)
\( {\textcolor{orange}{x}} = {\textcolor{midnightblue}{8}} \)
Ergebnis: Lösung immer als Punkt notieren.
\( \textsf{L}\big({\textcolor{orange}{8}} \mid {\textcolor{green}{2}}\big) \)

Textaufgaben mit dem Einsetzungsverfahren lösen

In Textaufgaben geht es darum zu erkennen, welche Größe sich sofort ausdrücken lässt.

Ansage: Beim Einsetzungsverfahren hast du meistens
→ zwei Größen (z. B. Alter, Strecke, Anzahl)
→ eine Beziehung, die eine Größe direkt beschreibt
Anna ist 4 Jahre älter als Ben.
Zusammen sind sie 28 Jahre alt.
Größe 1: Alter von Anna
Größe 2: Alter von Ben
Bedingung 1: Anna ist 4 Jahre älter
Bedingung 2: zusammen 28 Jahre
Ansage: Eine Größe lässt sich direkt beschreiben.
\( {\textcolor{green}{y}} \) = Alter von Ben
\( {\textcolor{orange}{x}} \) = Alter von Anna
\( \textsf{I.}\quad {\textcolor{orange}{x}} = {\textcolor{green}{y}} + 4 \)
\( \textsf{II.}\quad {\textcolor{orange}{x}} + {\textcolor{green}{y}} = 28 \)
→ eine Variable ist freigestellt
→ direkt einsetzbar
→ Einsetzungsverfahren
Noch ein typisches Beispiel:
Ein Rechteck ist 6 cm länger als breit.
Der Umfang beträgt 52 cm.
Größe 1: Länge
Größe 2: Breite
Bedingung 1: Länge = Breite + 6
Bedingung 2: Umfang 52 cm
Ansage: Wieder kann eine Größe direkt formuliert werden.
\( {\textcolor{green}{y}} \) = Breite
\( {\textcolor{orange}{x}} \) = Länge
\( \textsf{I.}\quad {\textcolor{orange}{x}} = {\textcolor{green}{y}} + 6 \)
\( \textsf{II.}\quad 2{\textcolor{orange}{x}} + 2{\textcolor{green}{y}} = 52 \)
→ eine Variable direkt beschrieben
→ Einsetzen statt Eliminieren
→ Einsetzungsverfahren
Merke
Typische Einsetzungsverfahren-Textaufgaben sind
Alters-, Geometrie- oder Beziehungsaufgaben.
Immer gilt:
→ zwei Größen
→ eine Größe lässt sich direkt ausdrücken
→ Einsetzen statt Addieren

Wusstest du schon…?

Das Einsetzungsverfahren ist deutlich älter als moderner Unterricht. Schon früh nutzte man es, um Zusammenhänge zu beschreiben, bei denen eine Größe von einer anderen abhängt.

Typisch waren Alters-, Weg- oder Mengenaufgaben: Eine Größe ist bekannt oder leicht ausdrückbar – und wird dann in eine zweite Beziehung eingesetzt.

Eine Variable wird durch einen Ausdruck ersetzt.
→ Eine Gleichung wird vereinfacht.
→ Übrig bleibt eine Rechnung mit nur einer Unbekannten.

Genau deshalb ist das Einsetzungsverfahren besonders übersichtlich: Man arbeitet Schritt für Schritt und verliert den Zusammenhang zwischen den Größen nicht aus dem Blick.

Und genau deshalb spielt es bis heute eine große Rolle in Textaufgaben, Klassenarbeiten und Prüfungen – immer dann, wenn sich eine Größe direkt beschreiben oder leicht umstellen lässt.

Deine Bildung, unsere Mission – made with ☕️  in Baden-Württemberg
Kontakt
Montag - Freitag:
13:00 -18:30 Uhr
+49 7321 7589939
Jobs
BenefitsJetzt bewerben
Social
©2025. OnMathe. Alle Rechte vorbehalten.
DatenschutzImpressum