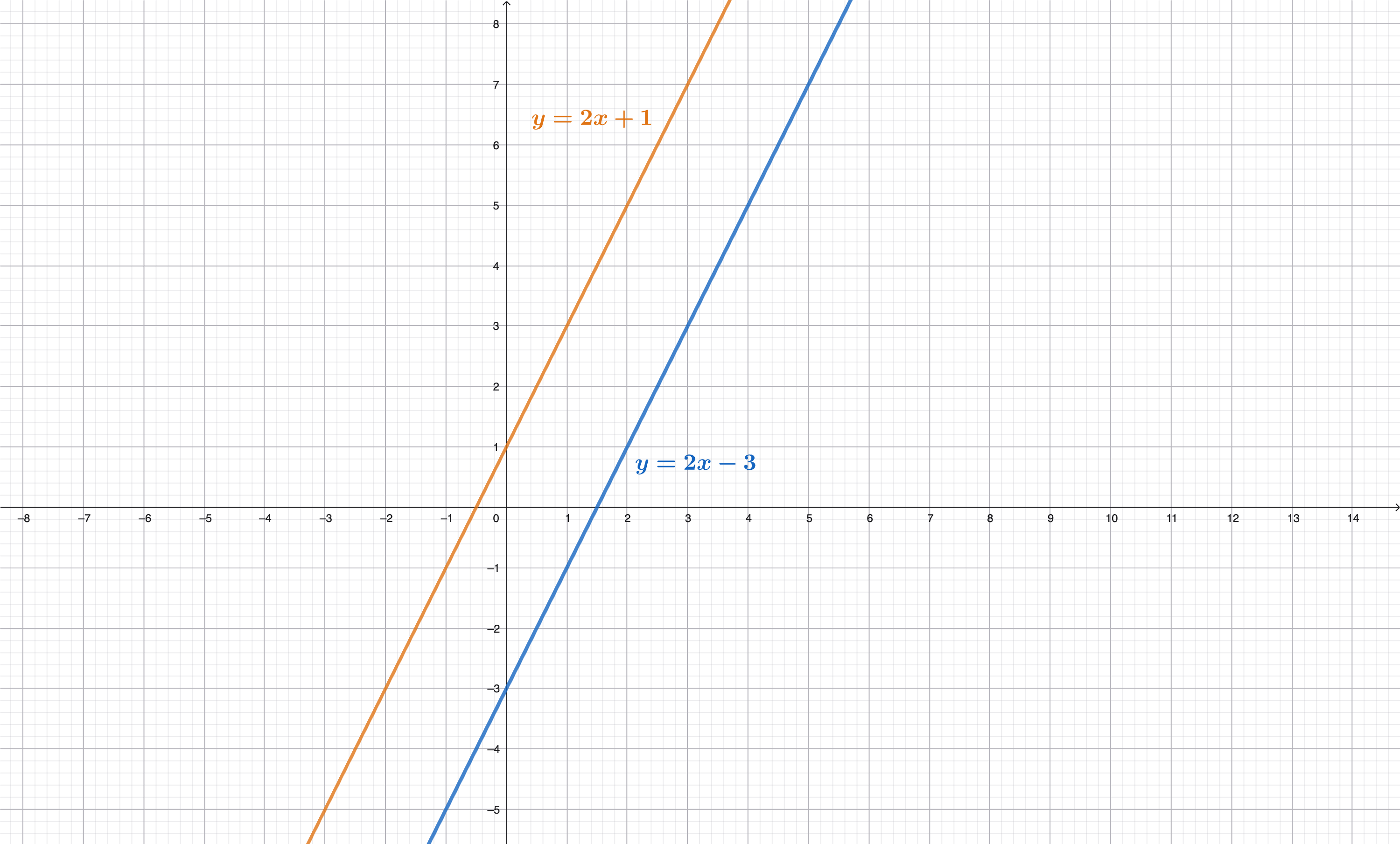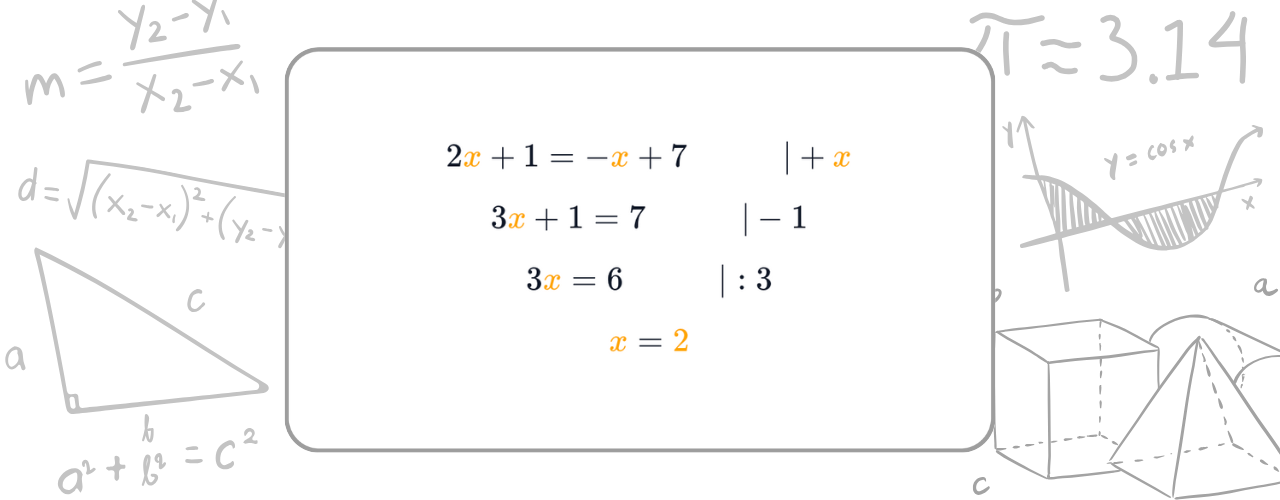Gleichungssysteme
lineare Gleichungssysteme lösen
Einleitung
Was ist ein LGS?
Hast du in einer linearen Gleichung zwei Unbekannte – also \(x\) und \(y\) –, kannst du sie nicht beide bestimmen. Du kannst nur eine Variable berechnen, wenn du den Wert der anderen bereits kennst.
Kennst du jedoch keine der beiden Variablen, brauchst du mehr Informationen, um sie zu berechnen – du benötigst eine zweite Gleichung. Zusammen bilden diese beiden Gleichungen ein lineares Gleichungssystem (kurz: LGS).
Du könntest jetzt beide Gleichungen in ein Koordinatensystem einzeichnen – denn es sich dabei um lineare Funktionen. Wenn du das machst, wirst du sehen, dass sich die beiden Geraden an einem Punkt schneiden. Genau dieser Schnittpunkt ist die Lösung des linearen Gleichungssystems.
Schauen wir uns das an einem Beispiel an. Hier siehst du zwei Gleichungen, die zusammen ein lineares Gleichungssystem bilden:
Wenn du diese beiden Geraden zeichnest, siehst du ihren Schnittpunkt bei \( {\color{green}{(1 \mid 3)}} \). Das bedeutet: \( {\color{green}{x = 1}} \) und \( {\color{green}{y = 3}} \) ist die Lösung des Gleichungssystems.
- Ein lineares Gleichungssystem besteht aus zwei Gleichungen mit denselben Variablen – meistens \(x\) und \(y\).
- Beide Gleichungen stehen für Geraden im Koordinatensystem.
- Die Lösung ist der Schnittpunkt dieser beiden Geraden.
- Im Schnittpunkt sind die Werte für \(x\) und \(y\) in beiden Gleichungen gleich.
Anzahl Lösungen im LGS
Ein lineares Gleichungssystem kann eine, keine oder unendlich viele Lösungen haben. Das hängt davon ab, wie die beiden Geraden im Koordinatensystem zueinander liegen.
- Eine Lösung: Die Geraden schneiden sich in einem Punkt. → Es gibt genau eine gemeinsame Lösung \((x \mid y)\).
- Keine Lösung: Die Geraden sind parallel – sie schneiden sich nie. → Das Gleichungssystem ist nicht lösbar.
- Unendlich viele Lösungen: Die Geraden liegen genau übereinander. → Jede Lösung der einen Gleichung gilt auch für die andere.
- Eine Lösung: Geraden schneiden sich → LGS lösbar.
- Keine Lösung: Geraden sind parallel → LGS nicht lösbar.
- Unendlich viele Lösungen: Geraden sind identisch → LGS hat unendlich viele Lösungen.
Das Gleichsetzungsverfahren
Das Einsetzungsverfahren
Das Additionsverfahren
Du suchst Profi-Nachhilfe mit echtem Impact? Dann bist du bei OnMathe genau richtig!
Ausgewählt für Dich
Empfohlene Beiträge
Mehr dazu
in unseren FAQs
1. Woran erkenne ich, ob ein LGS eine, keine oder unendlich viele Lösungen hat?
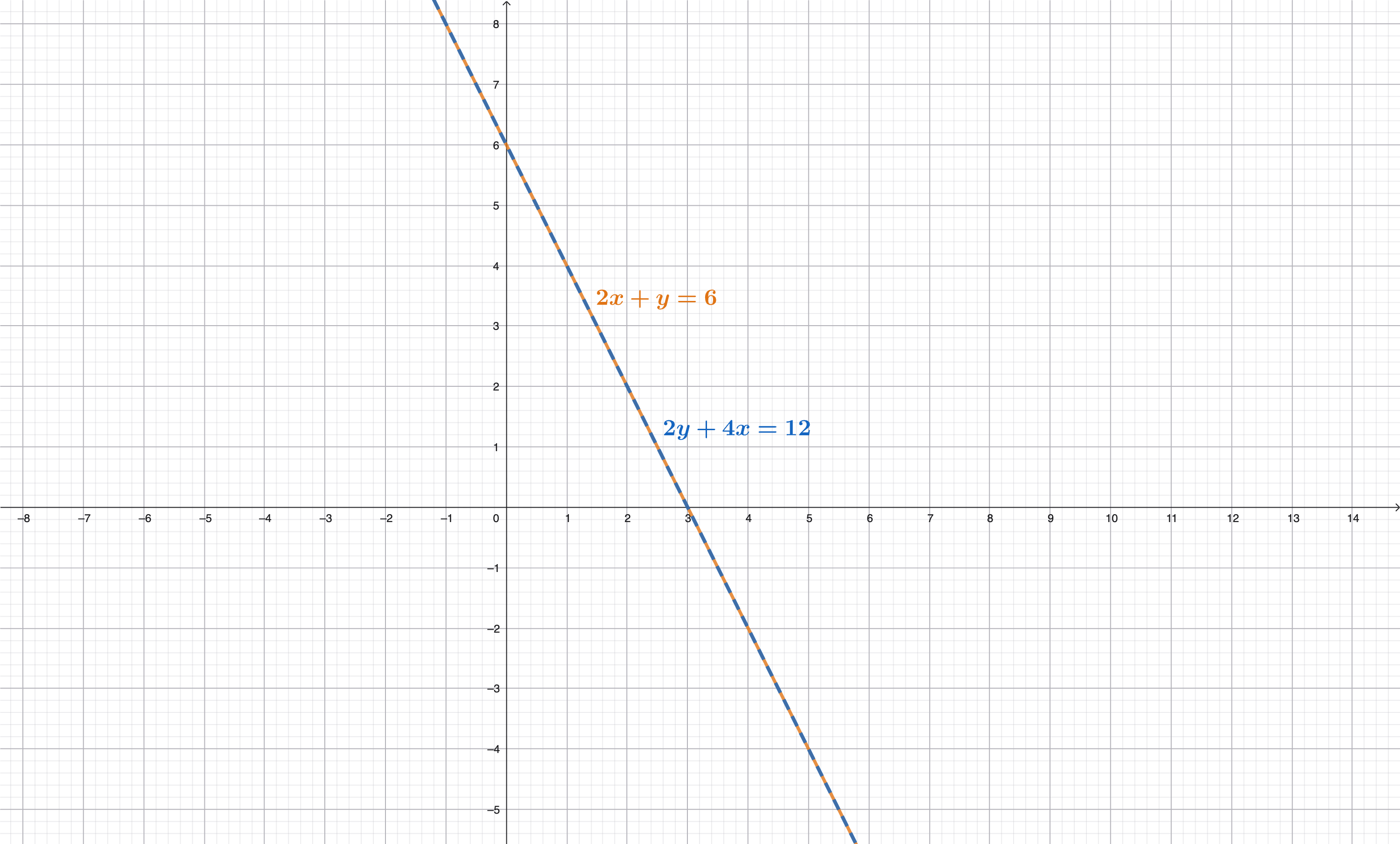
Schau dir die beiden Geraden im Koordinatensystem an: Schneiden sie sich, gibt es genau eine Lösung. Sind sie parallel, gibt es keine. Liegen sie übereinander, hat das LGS unendlich viele Lösungen.
2. Welches Verfahren ist das einfachste?
Das hängt vom Gleichungssystem ab. Wenn eine Gleichung schon nach einer Variablen aufgelöst ist, nimm das Einsetzungsverfahren. Wenn beide gleich aufgebaut sind, eignet sich das Gleichsetzungsverfahren. Wenn du durch geschicktes Addieren oder Subtrahieren eine Variable schnell entfernen kannst, nimm das Additionsverfahren.
3. Warum darf ich Gleichungen addieren oder subtrahieren?
Weil beide Gleichungen denselben Zusammenhang zwischen x und y beschreiben. Du veränderst damit nicht die Lösung, sondern kombinierst nur die Bedingungen, um eine Variable zu beseitigen.
4. Was bedeutet die Schreibweise L(x | y)?
Sie gibt den Schnittpunkt der beiden Geraden an – also die Werte von x und y, die beide Gleichungen erfüllen. Beispiel: L(2 | 3) bedeutet x = 2 und y = 3.
5. Was mache ich, wenn ich ein LGS mit drei Variablen habe?
Dann brauchst du auch drei Gleichungen, um alle Variablen bestimmen zu können. Du gehst ähnlich vor wie bei zwei Variablen – nur mit einem zusätzlichen Schritt.
Vertiefung
Weiterführende Informationen
Lineare Gleichungssysteme als Werkzeug
Lineare Gleichungssysteme, kurz LGS, sind ein wichtiges Werkzeug der Algebra. Mit ihnen kannst du Zusammenhänge zwischen zwei oder mehreren Variablen untersuchen und herausfinden, an welchem Punkt sich zwei lineare Funktionen schneiden. Ob in Physik, Wirtschaft oder Technik – überall, wo zwei Bedingungen gleichzeitig erfüllt werden müssen, kommen LGS ins Spiel.
Was ist ein lineares Gleichungssystem?
Ein LGS besteht aus zwei oder mehr linearen Gleichungen mit denselben Variablen, meist x und y. Jede Gleichung beschreibt eine Gerade im Koordinatensystem. Die Lösung ist der Punkt, an dem sich diese Geraden schneiden. Genau dort gelten beide Gleichungen gleichzeitig. Je nach Lage der Geraden kann es eine, keine oder unendlich viele Lösungen geben.
Mathematische Bedeutung
Lineare Gleichungssysteme helfen, komplexe Situationen auf einfache Rechenschritte zu reduzieren. Sie zeigen, wie mehrere Bedingungen voneinander abhängen und wie man mit logischem Denken und systematischem Vorgehen zu einer Lösung kommt. Sie bilden außerdem die Grundlage für viele Themen in der Oberstufe, etwa Matrizen, Vektoren oder lineare Optimierung.
Typische Stolperfallen und Lerntipps
Viele Schüler verwechseln das Gleichsetzungs- mit dem Einsetzungsverfahren oder vergessen, beim Einsetzen Klammern zu setzen. Achte auch darauf, dass die Vorzeichen korrekt bleiben, besonders beim Additionsverfahren. Ein guter Tipp: Wähle immer das Verfahren, das dir die einfachste Rechnung ermöglicht. Und überprüfe dein Ergebnis, indem du es in beide Gleichungen einsetzt – das sollte immer stimmen.
Ursprung und Entwicklung
Bereits im alten China wurden Gleichungssysteme mithilfe von Rechentafeln gelöst. Später entwickelten Mathematiker wie Gauß Methoden, um auch größere Systeme zu berechnen – heute bekannt als Gauß-Verfahren. Diese Techniken bilden die Grundlage moderner Computerprogramme, die mit Tausenden von Gleichungen arbeiten.
Moderne Anwendung
Lineare Gleichungssysteme finden sich überall im Alltag: in der Technik bei der Berechnung elektrischer Netzwerke, in der Wirtschaft bei Angebots- und Nachfrageanalysen oder in der Informatik bei der Programmierung von Simulationen. Auch in der Schule lernst du, sie zu verstehen und anzuwenden – eine Fähigkeit, die dich in vielen Bereichen weiterbringt.
