Mittlere & momentane Änderungsrate
Der Differenzenquotient
Einleitung
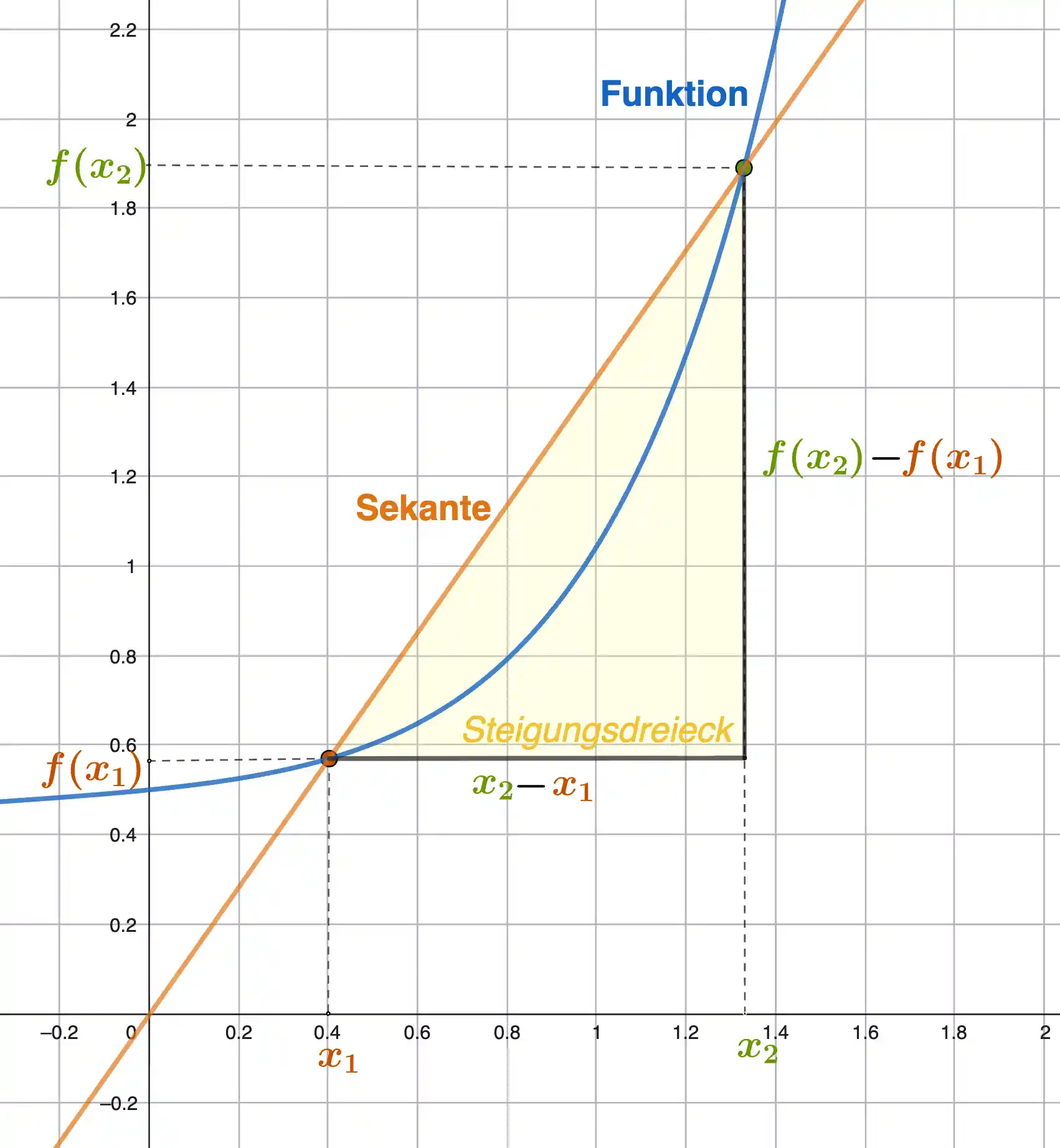
Was ist eine Sekante?
Die Sekante ist eine Gerade, also eine lineare Funktion. Sie schneidet den Funktionsgraphen in zwei Punkten.
Die Steigung der Sekante gibt die durchschnittliche Steigung des Graphen zwischen den beiden Schnittpunkten an.
Wichtig
Steigung der Sekante = Mittlere Änderungsrate
→ Wie steil ist der Graph
im Durchschnitt
zwischen \( {\textcolor{orangered}{x_1}} \) und \( {\textcolor{green}{x_2}} \)
→ durchschnittliche Änderung
pro Schritt in x-Richtung
Gegeben ist eine Sekante,
die den Graphen einer Funktion
in folgenden Punkten schneidet:
\( P_1({\textcolor{orangered}{1}} \mid {\textcolor{orangered}{1}})
\; und \;
P_2({\textcolor{green}{3}} \mid {\textcolor{green}{9}}) \)
Da die Sekante eine lineare Funktion ist,
berechnest du ihre Steigung
wie bei jeder Geraden der Form \( y = mx + b \).
\( m = \dfrac{\Delta y}{\Delta x} \)
\( m =
\dfrac{f({\textcolor{green}{x_2}}) - f({\textcolor{orangered}{x_1}})}
{{\textcolor{green}{x_2}} - {\textcolor{orangered}{x_1}}} \)
\( P_1({\textcolor{orangered}{1}} \mid {\textcolor{orangered}{1}})
\hspace{1.2cm}
P_2({\textcolor{green}{3}} \mid {\textcolor{green}{9}}) \)
\( P_1({\textcolor{orangered}{x_1}} \mid f({\textcolor{orangered}{x_1}}))
\hspace{0.5cm}
P_2({\textcolor{green}{x_2}} \mid f({\textcolor{green}{x_2}})) \)
\( m =
\dfrac{{\textcolor{green}{9}} - {\textcolor{orangered}{1}}}
{{\textcolor{green}{3}} - {\textcolor{orangered}{1}}} \)
\( m = \dfrac{8}{2} = 4 \)
Die Steigung der Sekante
beträgt 4.
Daraus folgt:
- 4 ist die mittlere Änderungsrate zwischen den beiden Punkten
- Also: die Funktion steigt im Durchschnitt um 4 pro x-Schritt nach rechts
Wichtig
Nicht:
Die Funktion steigt im gesamten Abschnitt
einmalig um diesen Wert.
Sondern:
Sie verändert sich
im Durchschnitt pro Schritt in x-Richtung
um diesen Wert.
Du willst das Steigungsdreieck bei linearen Funktionen
noch einmal wiederholen?
Dann schau dir unseren Beitrag
Lineare Funktionen
an.
Merke
Der Differenzenquotient
ist die Steigung einer linearen Funktion.
Diese Gerade heißt Sekante
und verbindet zwei Punkte des Graphen.
→ Sie beschreibt die durchschnittliche Steigung
zwischen diesen Punkten.
Differenzenquotient - Anwendung
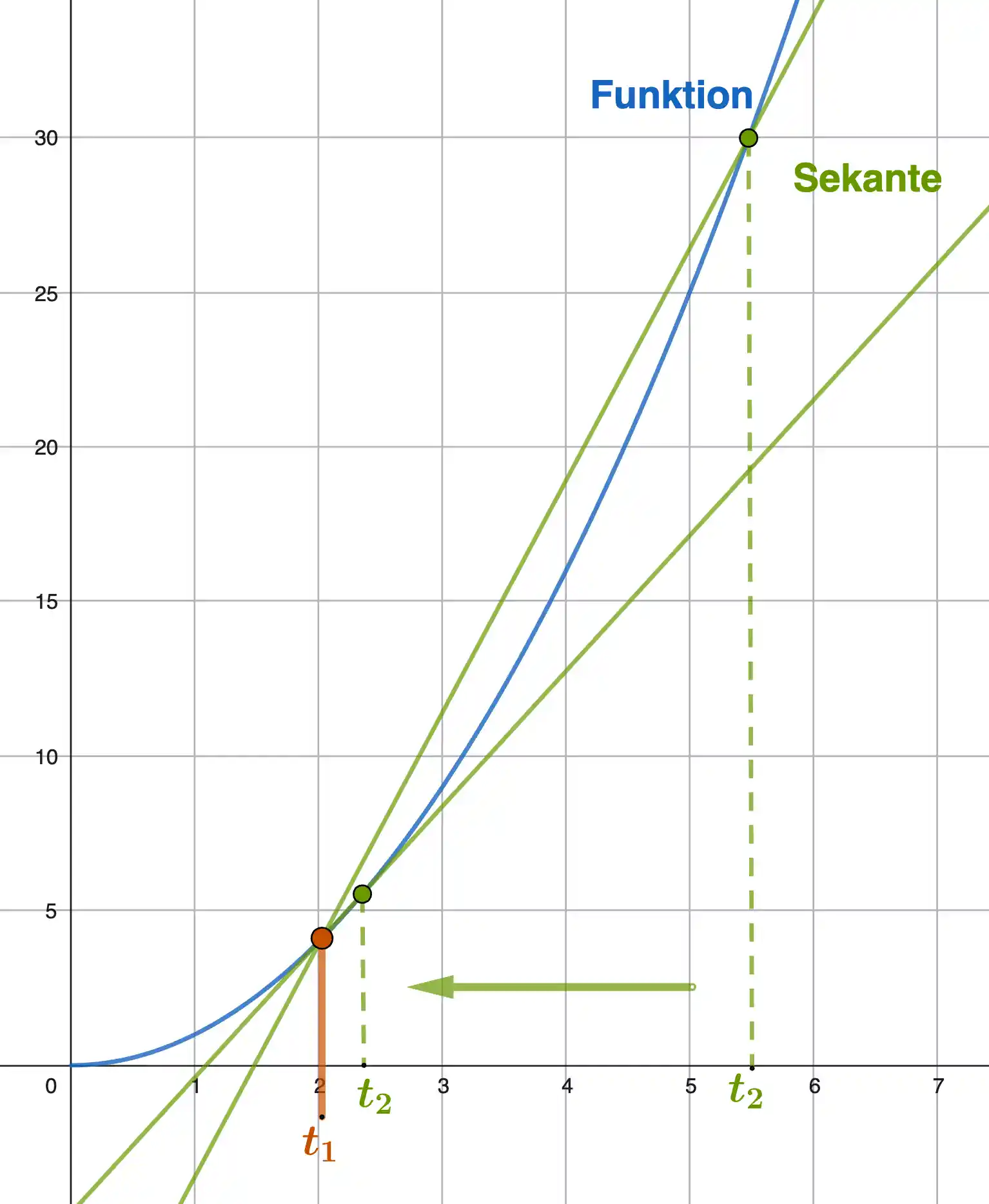
Grenzwert und momentane Änderung
Die Höhe einer Pflanze
(in cm) ist in Abhängigkeit von der Zeit
(in Tagen) gegeben:
\( h(x) = x^2 \)
Wie schnell wächst die Pflanze
genau bei
\( {\textcolor{orangered}{x}} = {\textcolor{orangered}{2}} \)?
Wir wollen wissen, wie schnell die Pflanze zu einem bestimmten Zeitpunkt wächst. Dafür betrachten wir zunächst einen Zeitraum — und verkleinern ihn Schritt für Schritt, bis wir die Änderung genau an einem Punkt erhalten.
Fester Punkt → \( {\textcolor{orangered}{a}} \) (hier ist \( {\textcolor{orangered}{a}} = {\textcolor{orangered}{2}} \))
Variabler Punkt → \( {\textcolor{green}{x}} \)
\({\textcolor{green}{x}} \) nähert sich \({\textcolor{orangered}{a}}\) an
→ Zeitraum wird immer kleiner
Wir bilden den Grenzwert für \( {\textcolor{green}{x}} \to {\textcolor{orangered}{a}} \). Das heißt, wir verringern den Abstand zwischen \({\textcolor{green}{x}} \) und \( {\textcolor{orangered}{a}} \), bis er praktisch nicht mehr sichtbar ist und erhalten die Steigung an genau einem Punkt.
Wichtig
Grenzwert bedeutet:
\( {\textcolor{green}{x}} \) kommt
\( {\textcolor{orangered}{a}} \)
immer näher, erreicht es aber nie ganz.
→ Der Abstand wird
beliebig klein,
aber nie null.
Was passiert grafisch?
Sekante:
schneidet den Graphen in
2 Punkten.
Wir bilden den Grenzwert:
\( {\textcolor{green}{x}} \to {\textcolor{orangered}{a}} \)
→ Die beiden Punkte
rücken zusammen.
→ Im Grenzfall bleibt
ein gemeinsamer Punkt.
→ Die Sekante wird zur
Tangente
(Gerade im Berührpunkt).
Merke
Tangente
→ berührt den Graphen in genau einem Punkt
→ Steigung im Berührpunkt = momentane Steigung
Sekante
→ schneidet den Graphen in zwei Punkten
→ Steigung zwischen zwei Punkten = durchschnittliche Steigung
Das setzen wir nun rechnerisch mit dem Grenzwert des Differenzenquotienten um.
1. Funktionswerte bestimmen
\( {\textcolor{orangered}{a}} = {\textcolor{orangered}{2}} \hspace{1cm} {\textcolor{green}{x}} = {\textcolor{green}{x}} \)
\( h({\textcolor{orangered}{2}}) = {\textcolor{orangered}{2}}^2 = {\textcolor{orangered}{4}} \)
\( h({\textcolor{green}{x}}) = {\textcolor{green}{x}}^2 \)
2. Differenzenquotient aufstellen
\( m = \lim\limits_{{\textcolor{green}{x}} \to {\textcolor{orangered}{2}}}
\dfrac{h({\textcolor{green}{x}}) - h({\textcolor{orangered}{a}})}
{{\textcolor{green}{x}} - {\textcolor{orangered}{a}}} \)
3. Einsetzen
\( m = \lim\limits_{{\textcolor{green}{x}} \to {\textcolor{orangered}{2}}}
\dfrac{{\textcolor{green}{x}}^2 - {\textcolor{orangered}{4}}}
{{\textcolor{green}{x}} - {\textcolor{orangered}{2}}} \)
4. Zähler umformen (3. binomische Formel)
\( {\textcolor{green}{x}}^2 - {\textcolor{orangered}{4}}
= ({\textcolor{green}{x}} - 2)\,({\textcolor{green}{x}} + 2) \)
Jetzt können wir ({\textcolor{green}{x}} - 2) kürzen
\( m = \lim\limits_{{\textcolor{green}{x}} \to {\textcolor{orangered}{2}}}
\dfrac{\cancel{({\textcolor{green}{x}} - 2)}\,({\textcolor{green}{x}} + 2)}
{\cancel{{\textcolor{green}{x}} - {\textcolor{orangered}{2}}}} \)
\( m = \lim\limits_{{\textcolor{green}{x}} \to {\textcolor{orangered}{2}}} ({\textcolor{green}{x}} + 2) \)
Mit Kürzen entfernen wir den Nenner und verhindern \( 2 - 2 = 0 \)
→ durch 0 teilen ist nicht erlaubt
→ durch 0 teilen ist nicht erlaubt
5. Grenzwert bilden
für
\( {\textcolor{green}{x}} \to {\textcolor{orangered}{2}} \).
\( m = \lim\limits_{{\textcolor{green}{x}} \to {\textcolor{orangered}{2}}}
({\textcolor{green}{x}} + 2) \)
Jetzt dürfen wir einsetzen, denn \( {\textcolor{green}{x}} \to {\textcolor{orangered}{2}} \):
\( m = {\textcolor{orangered}{2}} + {\textcolor{orangered}{2}} \)
\( m = 4 \)
→ Zum Zeitpunkt
\( {\textcolor{orangered}{x}} = {\textcolor{orangered}{2}} \)
(also am zweiten Tag)
beträgt die momentane Wachstumsgeschwindigkeit der Pflanze
4 cm pro Tag.
Wichtig
Grenzwert bilden:
\( {\textcolor{green}{x}} \to {\textcolor{orangered}{a}} \)
Einsetzen würde im Nenner ergeben →
\( {\textcolor{orangered}{a}} - {\textcolor{orangered}{a}} = 0 \)
→ Division durch 0
ist nicht definiert
⇒ Deshalb umformen und kürzen
Merke
Differenzenquotient
→ durchschnittliche Steigung
Grenzwert des Differenzenquotienten
→ Differentialquotient
Differentialquotient
→ momentane Steigung
\(
\lim\limits_{{\textcolor{green}{x_2}} \to {\textcolor{orangered}{x_1}}}
\dfrac{f({\textcolor{green}{x_2}}) - f({\textcolor{orangered}{x_1}})}
{{\textcolor{green}{x_2}} - {\textcolor{orangered}{x_1}}}
\)
So umständlich bleibt das nicht: Mit den Ableitungsregeln geht das deutlich schneller.
Du suchst Profi-Nachhilfe mit echtem Impact? Dann bist du bei OnMathe genau richtig!
Ausgewählt für Dich
Empfohlene Beiträge
Mehr dazu
in unseren FAQs
Was ist der Unterschied zwischen Differenzenquotient und Differentialquotient?
Warum brauche ich zwei Punkte für den Differenzenquotienten?
Warum kann man die momentane Steigung nicht direkt berechnen?
Was bedeutet der Grenzwert beim Differentialquotienten?
Warum ist die h-Methode so wichtig?
Mehr dazu
Weiterführende Informationen
Die h-Methode
Vom Differenzenquotient zur Ableitung
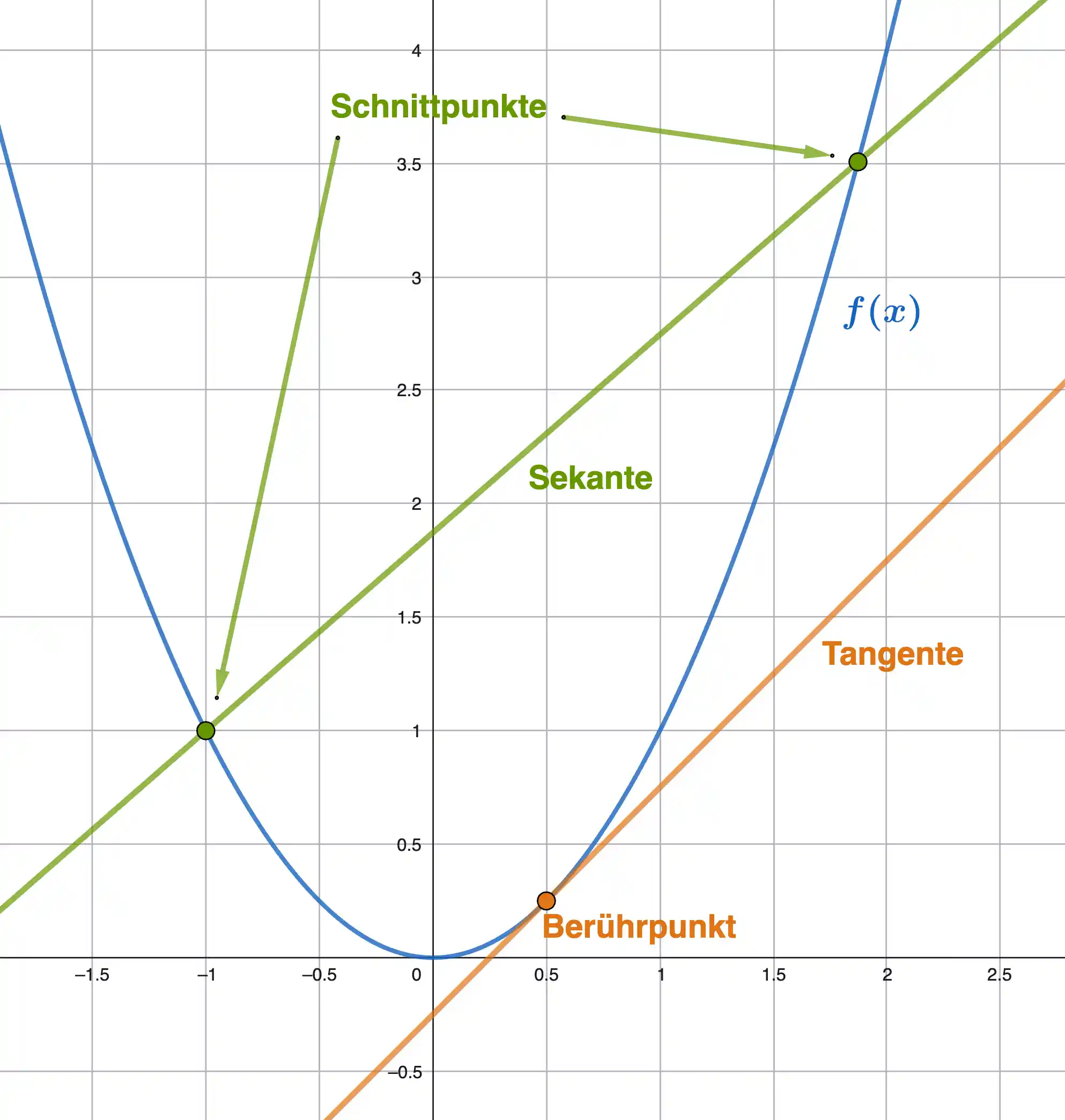
Sekante vs. Tangente
Bisher haben wir Steigungen rechnerisch bestimmt. Im Bild siehst du jetzt, was geometrisch dahintersteckt.
Im Bild siehst du eine Sekante und eine Tangente an einer Funktion.
\(\textcolor{green}{Sekante}\):
schneidet den Funktionsgraphen
in zwei Punkten.
→ Beschreibt die mittlere Änderung
zwischen zwei Stellen.
→ Rechnerisch:
Differenzenquotient.
\(\textcolor{orange}{Tangente}\):
berührt den Funktionsgraphen
in genau einem Punkt.
→ Beschreibt die momentane Änderung
an dieser Stelle.
→ Rechnerisch:
Differentialquotient
bzw. Ableitung.
Merke
\(\textcolor{green}{Sekante}\)
→ zwei Punkte → mittlere Steigung →
Differenzenquotient
\(\textcolor{orange}{Tangente}\)
→ ein Punkt → momentane Steigung →
Differentialquotient
Die Sekante und die Tangente sind keine Gegensätze. Die Tangente entsteht als Grenzfall aus der Sekante.
Eine Sekante verbindet
zwei verschiedene Punkte
des Funktionsgraphen.
Wir wählen den zweiten Punkt
\( {\textcolor{green}{x_2}} \)
immer näher bei
\( {\textcolor{orangered}{x_1}} \).
→ Zu jedem Abstand entsteht
eine neue Sekante.
Lässt man
\( {\textcolor{green}{x_2}} \)
gegen
\( {\textcolor{orangered}{x_1}} \)
laufen,
bilden wir einen Grenzwert.
Im Grenzfall fallen beide Punkte
zusammen.
→ Die Sekante geht
in die \(\textcolor{orange}{Tangente}\)
über.
Dieser Grenzwert beschreibt die
momentane Steigung
an einer Stelle.
Wichtig
\(\textcolor{green}{Sekante}\):
mittlere Steigung
zwischen
\( {\textcolor{orangered}{x_1}} \)
und
\( {\textcolor{green}{x_2}} \)
→
\( {\textcolor{green}{x_2}} \)
nähert sich
\( {\textcolor{orangered}{x_1}} \)
an
(Grenzwert)
→
momentane Steigung
an der Stelle
\( {\textcolor{orangered}{x_1}} \)
→
\(\textcolor{orange}{Tangente}\)
Vertiefung
